
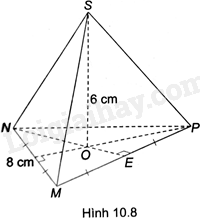
Cho hình chóp tam giác đều S.MNP có cạnh đáy bằng 8cm, đường cao bằng 6cm (H.10.8). Hãy tính thể tích của hình chóp S.MNP. Cho biết $\sqrt{48}\approx 6,9$

Sử dụng kiến thức về thể tích của hình chóp tam giác đều để tính thể tích hình chóp tam giác đều S. MNP: Thể tích của hình chóp tam giác đều bằng $\frac{1}{3}$ tích của diện tích đáy với chiều cao của nó.

Advertisements (Quảng cáo)
Gọi NE là đường trung tuyến của tam giác MNP và O là giao điểm của hai đường trung tuyến trong tam giác MNP. Do đó SO là chiều cao của hình chóp nên $SO=6cm$
Tam giác MNP là tam giác đều nên NE là đường trung tuyến đồng thời là đường cao. Do đó, $ME=EP=\frac{1}{2}MP=4\left( cm \right)$
Tam giác MEN vuông tại E nên $M{{E}^{2}}+N{{E}^{2}}=M{{N}^{2}}$ (định lí Pythagore)
$N{{E}^{2}}=64-16=48$ nên $NE=\sqrt{48}\approx 6,9\left( cm \right)$
Thể tích của hình chóp S.MNP là:
$V=\frac{1}{3}{{S}_{MNE}}.SO=\frac{1}{3}.\frac{1}{2}.MN.NE.SO=\frac{1}{6}.8.6,9.6=55,2\left( c{{m}^{3}} \right)$
