
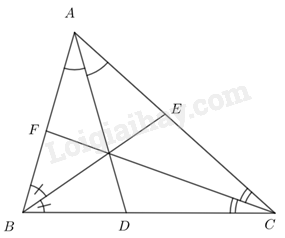
Cho tam giác ABC có ba đường phân giácAD, BE, CF. Biết \(AB = 4,\,\,BC = 5,\,\,CA = 6\). Tính BD, CE, AF.

Dựa vào tính chất đường phân giác để tính độ dài các cạnh.

Advertisements (Quảng cáo)
Có AD là đường phân giác trong tam giác ABC nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}} \Rightarrow \frac{{DB}}{{DC}} = \frac{4}{6} = \frac{2}{3} \Rightarrow DC = \frac{3}{2}DB\)
Mà \(DB + DC = BC \Rightarrow DB + \frac{3}{2}DB = 5 \Rightarrow DB = 2\)
Có BE là đường phân giác trong tam giác ABC nên \(\frac{{AE}}{{EC}} = \frac{{AB}}{{CB}} \Rightarrow \frac{{AE}}{{EC}} = \frac{4}{5} \Rightarrow AE = \frac{4}{5}CE\)
Mà \(AE + EC = AC \Rightarrow \frac{4}{5}CE + CE = 6 \Rightarrow CE = \frac{{10}}{3}\)
Có CF là đường phân giác trong tam giác ABC nên \(\frac{{AF}}{{FB}} = \frac{{CA}}{{CB}} \Rightarrow \frac{{AF}}{{FB}} = \frac{6}{5} \Rightarrow FB = \frac{6}{5}AF\)
Mà \(AF + FB = AB \Rightarrow AF + \frac{5}{6}AF = 4 \Rightarrow AF = \frac{{24}}{{11}}\).
