
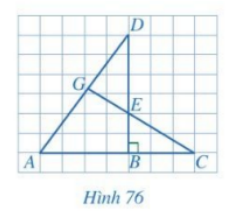
Cho Hình 76, biết \(AB = 4,\,\,BC = 3,\,\,BE = 2,\,\,BD = 6\). Chứng minh:
a) \(\Delta ABD \backsim \Delta EBC\)
b) \(\widehat {DAB} = \widehat {DEG}\)
c) Tam giác DGE vuông

a) Chứng minh hai tam giác đồng dạng bằng trường hợp đồng dạng thứ hai.
b) Từ hai tam giác đồng dạng đã chứng minh ở câu a suy ra các cặp góc bằng nhau.
c) Chứng minh \(\widehat {DGE} = 90^\circ \)

a) Ta có: \(\frac{{AB}}{{EB}} = \frac{4}{2} = 2;\,\,\frac{{BD}}{{BC}} = \frac{6}{3} = 2\)
Advertisements (Quảng cáo)
\( \Rightarrow \frac{{AB}}{{EB}} = \frac{{BD}}{{BC}}\)
Xét tam giác ABD và tam giác EBC có:
\(\frac{{AB}}{{EB}} = \frac{{BD}}{{BC}}\) và \(\widehat {ABD} = \widehat {EBC} = 90^\circ \)
\( \Rightarrow \Delta ABD \backsim \Delta EBC\) (c-g-c).
b) Vì \(\Delta ABD \backsim \Delta EBC\) nên \(\widehat {DAB} = \widehat {CEB}\)
Mà \(\widehat {DEG} = \widehat {CEB}\) (hai góc đối đỉnh) nên \(\widehat {DAB} = \widehat {DEG}\).
c) Vì \(\Delta ABD \backsim \Delta EBC\) nên \(\widehat {ADB} = \widehat {ECB}\) hay \(\widehat {GDE} = \widehat {ECB}\)
Vì tam giác EBC vuông tại B nên ta có:
\(\begin{array}{l}\widehat {ECB} + \widehat {CEB} = 90^\circ \\ \Rightarrow \widehat {GDE} + \widehat {DEG} = 90^\circ \end{array}\)
Mà trong tam giác DEG có:
\(\begin{array}{l}\widehat {GDE} + \widehat {DEG} + \widehat {DGE} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DGE} = 180^\circ \\ \Rightarrow \widehat {DGE} = 90^\circ \end{array}\)
\( \Rightarrow \)Tam giác DGE vuông tại G.
