
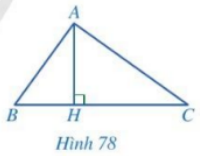
Cho Hình78, biết \(A{H^2} = BH.CH\). Chứng minh:
a) \(\Delta HAB \backsim \Delta HCA\)
b) Tam giác ABC vuông tại A.

a) Từ đẳng thức đã cho, suy ra tỉ lệ các đoạn thẳng rồi chứng minh hai tam giác bằng nhau theo trường hợp thứ hai.
b) Chứng minh \(\widehat {BAC} = 90^\circ \)

Advertisements (Quảng cáo)
a) Ta có:
\(A{H^2} = BH.CH \Rightarrow AH.AH = BH.CH \Rightarrow \frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\)
Xét tam giác HAB và tam giác HCA có:
\(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\) và \(\widehat {AHB} = \widehat {CHA} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HCA\) (c-g-c)
b) Vì \(\Delta HAB \backsim \Delta HCA\)nên \(\widehat {HBA} = \widehat {HAC}\)
Xét tam giác AHB vuông tại H có:
\(\begin{array}{l}\widehat {HAB} + \widehat {HBA} = 90^\circ \\ \Rightarrow \widehat {HAB} + \widehat {HAC} = 90^\circ \\ \Rightarrow \widehat {BAC} = 90^\circ \end{array}\)
Vậy tam giác ABC vuông tại A.
