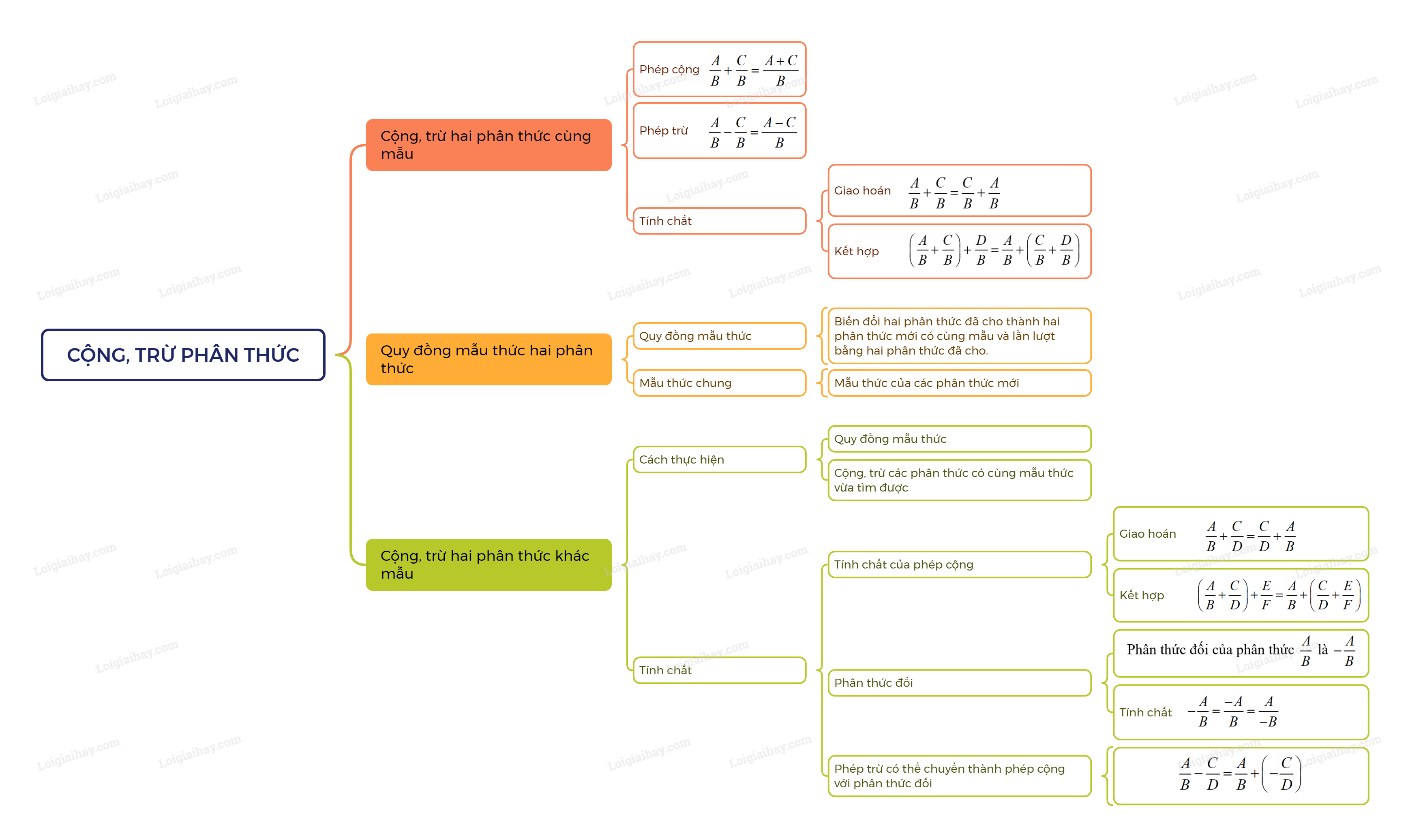
1. Cộng, trừ hai phân thức cùng mẫu
Muốn cộng (hoặc trừ) hai phân thức có cùng mẫu thức, ta cộng (hoặc trừ) các tử thức với nhau và giữ nguyên mẫu thức.
\(\frac{A}{B} + \frac{C}{B} = \frac{{A + C}}{B}; \frac{A}{B} - \frac{C}{B} = \frac{{A - C}}{B}\)
Chú ý: Phép cộng phân thức có các tính chất giao hoán, kết hợp tương tự như đối với phân số.
Ví dụ:
\(\begin{array}{l}\frac{{x + y}}{{xy}} + \frac{{x - y}}{{xy}} = \frac{{x + y + x - y}}{{xy}} = \frac{{2x}}{{xy}} = \frac{2}{y}\\\frac{x}{{x + 3}} + \frac{{2 - x}}{{x + 3}} = \frac{{x + 2 - x}}{{x + 3}} = \frac{2}{{x + 3}}\end{array}\)
2. Cộng, trừ hai phân thức khác mẫu
Quy đồng mẫu thức hai phân thức
Quy đồng mẫu thức hai phân thức là biến đổi hai phân thức đã cho thành hai phân thức mới có cùng mẫu thức và lần lượt bằng hai mẫu thức đã cho.
Mẫu thức chung
Mẫu thức của các phân thức mới đó gọi là mẫu thức chung của hai phân thức đã cho.
Advertisements (Quảng cáo)
Cộng, trừ hai phân thức khác mẫu
Muốn cộng, trừ hai phân thức khác mẫu thức, ta thực hiện các bước:
- Quy đồng mẫu thức;
- Cộng, trừ các phân thức có cùng mẫu thức vừa tìm được.
Chú ý:
a. Phép cộng các phân thức cũng có các tính chất giao hoán, kết hợp:
\(\frac{A}{B} + \frac{C}{D} = \frac{C}{D} + \frac{A}{B}; \left( {\frac{A}{B} + \frac{C}{D}} \right) + \frac{E}{F} = \frac{A}{B} + \left( {\frac{C}{D} + \frac{E}{F}} \right)\).
b. Phân thức đối của phân thức \(\frac{A}{B}\) là \( - \frac{A}{B}\). Ta có tính chất \( - \frac{A}{B} = \frac{{ - A}}{B} = \frac{A}{{ - B}}\,\).
c. Phép trừ phân thức có thể chuyển thành phép cộng với phân thức đối: \(\frac{A}{B} - \frac{C}{D} = \frac{A}{B} + \left( { - \frac{C}{D}} \right)\)