
a) Vẽ đồ thị của hàm số \(y = x\) và \(y = x + 2\) trên cùng một mặt phẳng tọa độ.
b) Dùng thước đo góc để tìm góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\).

- Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\). Đồ thị hàm số \(y = ax\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(A\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(B\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A\) và \(B\). Đồ thị của hàm số \(y = ax + b\) là đường thẳng đi qua hai điểm \(A\) và \(B\).

Advertisements (Quảng cáo)
a)
- Vẽ đồ thị hàm số \(y = x\).
Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).
Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Vẽ đồ thị hàm số \(y = x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} = - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
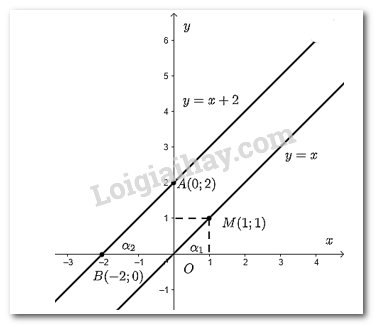
b) Góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).
Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).
