Một người đi bộ trên đường thẳng với tốc độ \(v\left( {km/h} \right)\). Gọi \(s\left( {km} \right)\) là quãng đường đi được trong \(t\left( h \right)\).
a)
a) Lập công thức tính \(s\) theo \(t\).

- Công thức tính quãng đường: \(s = v.t\)

Cứ 1 giờ người đó lại đi được \(v\) km.
Cứ 2 giờ người đó lại đi được \(2v\)km.
Vậy sau \(t\left( h \right)\) người đó sẽ đi được quãng đường \(v.t\) km.
Vậy ta có công thức tính \(s\)theo \(t\) như sau: \(s = v.t\) trong đó \(v\) là vận tốc, \(t\) là thời gian và \(s\) là quãng đường đi được.
b)
Advertisements (Quảng cáo)
b) Vẽ đồ thị của hàm số \(s\) theo \(t\) khi \(v = 4\).

- Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\). Đồ thị hàm số \(y = ax\) là đường thẳng đi qua hai điểm \(O\) và \(M\).

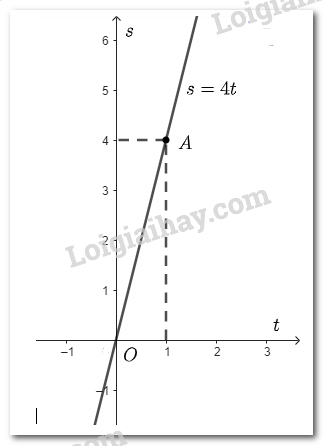
Với \(v = 4 \Rightarrow s = 4t\). Khi đó \(s\) là hàm số bậc nhất theo biến \(t\).
Với \(t = 1 \Rightarrow s = 4.1 = 4 \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;4} \right)\).
Đồ thị hàm số \(s = 4t\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;4} \right)\).