
Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.
a) Chứng minh rằng AE = DF.
b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.

a. Chứng minh tứ giác ADEF là hình chữ nhật, suy ra hai đường chéo AE = DF.
b. Chứng minh BDFE là hình bình hành, suy ra 2 đường chéo cắt nhau tại trung điểm, nên I nằm giữa B và F suy ra B, I, F thẳng hàng.

Cách 1.
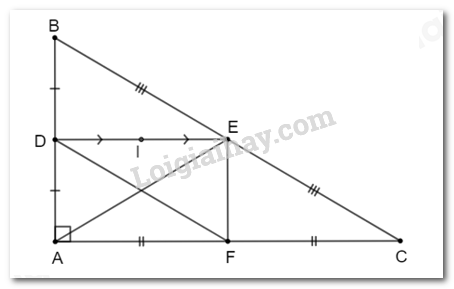
a) Theo đề bài, tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^o}\) hay AB ⊥ AC.
Vì D, E lần lượt là trung điểm của AB, BC nên DE là đường trung bình của tam giác ABC suy ra DE // AC.
Mà AB ⊥ AC nên AB ⊥ DE hay \(\widehat {A{\rm{D}}E} = {90^o}\).
Tương tự, ta chứng minh được: EF ⊥ AC hay \(\widehat {AEF} = {90^o}\)
Ta có: \(\widehat {BAC} + \widehat {A{\rm{D}}E} + \widehat {AFE} + \widehat {DEF} = {360^o}\)
90°+90°+90o\( + \widehat {DEF}\) = 360o 270°+ \(\widehat {DEF}\)=360°
Suy ra \(\widehat {DEF}\)=360°−270°=90o
Tứ giác ADEF có \(\widehat {BAC} = {90^o};\widehat {A{\rm{D}}E} = {90^o};\widehat {AEF} = {90^o};\widehat {DEF} = {90^{^o}}\)
Do đó tứ giác ADEF là hình chữ nhật.
Suy ra hai đường chéo AE và DF bằng nhau.
Advertisements (Quảng cáo)
Vậy AE = DF (đpcm).
b) Vì D, F lần lượt là trung điểm của AB, AC nên DF là đường trung bình của tam giác ABC.
Suy ra DF // BC hay DF // BE.
Vì tứ giác ADEF là hình chữ nhật nên AD // EF hay BD // EF.
Tứ giác BDFE có DF // BE và BD // EF nên tứ giác BDFE là hình bình hành.
Hình bình hành BDFE có hai đường chéo BF và DE.
Mà I là trung điểm của DE nên I cũng là trung điểm của BF.
Do đó, ba điểm B, I, F thẳng hàng.
Cách 2.
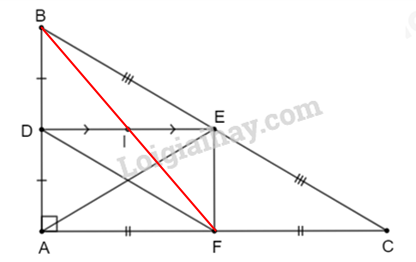
a) Tam giác ABC vuông tại A, AE là tiếp tuyến (gt)
=> \(AE = \frac{1}{2}BC\) (1)
D, F lần lượt là trung điểm của AB, AC (gt)
=> \(DF = \frac{1}{2}BC\) (2)
Từ (1) và (2) => AE = DF.
b) DF là đường trung bình của tam giác ABC (cmt)
=> DF // BE (DF //BC) và DF = BE (DF = \(\frac{1}{2}\)BC = BE).
=> Tứ giác BDFE là hình bình hành => DE và BF cắt nhau tại trung điểm của mỗi đường.
I là trung điểm của DE (gt) => I là trung điểm của BF => B, I, F thẳng hàng.
