
Cho tam giác ABC vuông tại A có AB=5cm, AC=4cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB
a) Chứng minh rằng ΔHDA ∽ ΔAHC
b) Tính độ dài các đoạn thẳng HA, HB, HC, HD

a) Chứng minh tam giác vuông HDA (vuông tại D) và tam giác vuông AHC (vuông tại H) có: \(\widehat {DHA} = \widehat {HAC}\)
b) Áp dụng định lý Pythagore trong tam giác vuông để tính HA, HB, HC, HD

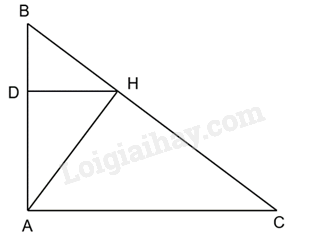
a) Có AB ⊥ AC, HD ⊥ AB
Suy ra HD // AC
Suy ra \(\widehat {DHA} = \widehat {HAC}\)
- Xét tam giác vuông HDA (vuông tại D) và tam giác vuông AHC (vuông tại H) có: \(\widehat {DHA} = \widehat {HAC}\)
Suy ra ΔHDA ∽ ΔAHC
Advertisements (Quảng cáo)
b) Xét tam giác ABC có: \(A{B^2} + A{C^2} = B{C^2}\)
mà AB=5cm, AC=4cm
Suy ra \(BC = \sqrt {41} \)
- Có AH.BC=AB.AC
Suy ra \(AH = \frac{{20\sqrt {41} }}{{41}}\)
Suy ra \(H{B^2} = A{B^2} - A{H^2}\) (áp dụng định lý Pythagore trong tam giác vuông BHA)
Suy ra \(HB = \frac{{25\sqrt {41} }}{{41}}\)
Suy ra \(HC = \frac{{16\sqrt {41} }}{{41}}\)
- Xét tam giác vuông BDH và tam giác vuông BAC có: HD // AC
Suy ra ΔBDH ∽ ΔBAC
Suy ra \(\frac{{BH}}{{BC}} = \frac{{DH}}{{AC}}\)
Suy ra \(H{\rm{D}} = \frac{{100}}{{41}}\)
