
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
a) \(\frac{{B{\rm{D}}}}{{BC}} = \frac{{AB}}{{AB + AC}}\), từ đó suy ra \(A{\rm{E}} = \frac{{AB.AC}}{{AB + AC}}\)
b) ΔDFC ∽ ΔABC
c) DF=DB
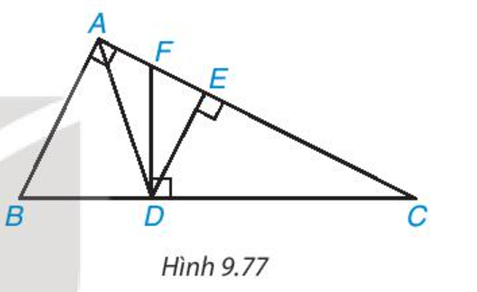

Sử dụng các tam giác đồng dạng để chứng minh

a) Vì AD là tia phân giác của góc BAC \( \Rightarrow \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} \Rightarrow DB.AC = DC.AB(*)\)
Advertisements (Quảng cáo)
Ta có: \(B{\rm{D}}.\left( {AB + AC} \right) = B{\rm{D}}.AB + B{\rm{D}}.AC = DB.AB + DC.AB = AB.\left( {DB + DC} \right) = AB.BC\)
\(\begin{array}{l} \Rightarrow B{\rm{D}}.\left( {AB + AC} \right) = AB.BC\\ \Rightarrow \frac{{B{\rm{D}}}}{{BC}} = \frac{{AB}}{{AB + AC}}(1)\end{array}\)
\(\Delta CE{\rm{D}} \backsim \Delta CAB\left( {{{\widehat C}^{}}chung{;^{}}\widehat A = \widehat E} \right)\)
\(\begin{array}{l} \Rightarrow \frac{{CE}}{{CA}} = \frac{{C{\rm{D}}}}{{CB}}\\ \Rightarrow \frac{{AC - A{\rm{E}}}}{{AC}} = \frac{{BC - B{\rm{D}}}}{{BC}} \Rightarrow 1 - \frac{{A{\rm{E}}}}{{AC}} = 1 - \frac{{DB}}{{BC}}\\ \Rightarrow \frac{{A{\rm{E}}}}{{AC}} = \frac{{DB}}{{BC}}(2)\end{array}\)
Từ (1), (2) suy ra: \(\frac{{A{\rm{E}}}}{{AC}} = \frac{{AB}}{{AB + AC}} \Rightarrow A{\rm{E}} = \frac{{AB.AC}}{{AB + AC}}\)
b)
\(\begin{array}{l}\Delta DFC \backsim \Delta ABC\\ \Rightarrow \frac{{DF}}{{AB}} = \frac{{DC}}{{AC}} \Rightarrow DF = \frac{{AB.DC}}{{AC}}(3)\end{array}\)
Từ (*) ta có: \(DB = \frac{{DC.AB}}{{AC}}(4)\)
Từ (3), (4) suy ra: DF = DB
