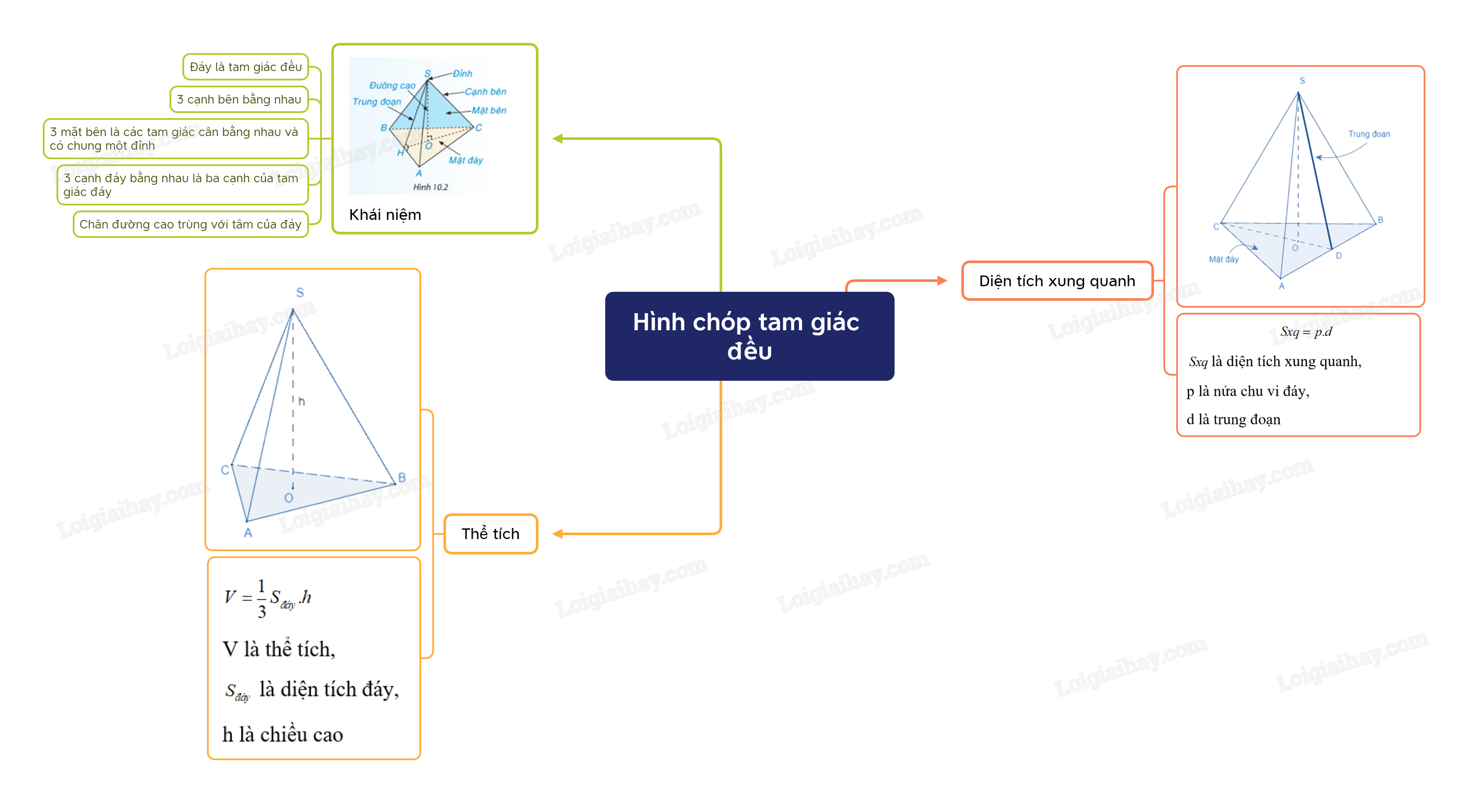
1. Định nghĩa
Hình chóp tam giác đều có:
- Đáy là tam giác đều.
- 3 cạnh bên bằng nhau.
- 3 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 3 cạnh đáy bằng nhau là ba cạnh của tam giác đáy.
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của tam giác đáy.
2. Diện tích xung quanh và thể tích của hình chóp tam giác đều
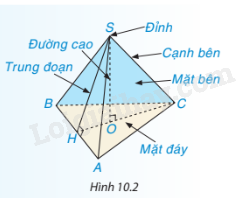
a. Diện tích xung quanh của hình chóp tam giác đều
Diện tích xung quanh, kí hiệu là \({S_{xq}}\) của hình chóp tam giác đều được tính theo công thức:
\({S_{xq}} = p.d\),
trong đó p là nửa chu vi đáy, d là trung đoạn.
Advertisements (Quảng cáo)
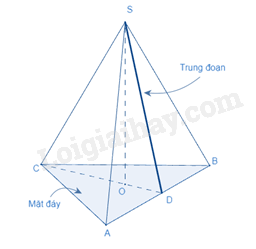
b. Thể tích của hình chóp tam giác đều
Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) diện tích đáy nhân với chiều cao.
\(V = \frac{1}{3}S.h\)
trong đó V là thể tích,
S là diện tích đáy,
h là chiều cao.
Ví dụ: Cho hình chóp tam giác đều sau:
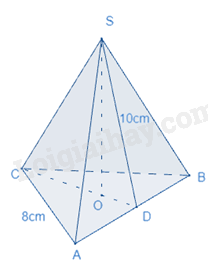
Diện tích xung quanh của hình chóp là: \({S_{xq}} = \frac{{3.8}}{2}.10 = 120(c{m^2})\)
\(\begin{array}{l}CD = \sqrt {{8^2} - {{\left( {\frac{8}{2}} \right)}^2}} = 4\sqrt 3 \\OD = \frac{1}{3}CD = \frac{1}{3}.4\sqrt 3 = \frac{{4\sqrt 3 }}{3}\\SO = \sqrt {{{10}^2} - {{\left( {\frac{{4\sqrt 3 }}{3}} \right)}^2}} = \frac{{2\sqrt {213} }}{3}\\\end{array}\)
Thể tích của hình chóp là: \(V = \frac{1}{3}.SO.\frac{1}{2}CD.AB = \frac{1}{3}.\frac{{2\sqrt {213} }}{3}.\frac{1}{2}.4\sqrt 3 .8 = \frac{{32\sqrt {71} }}{3}\).