1. Tính chất cơ bản của phân thức
- Tính chất cơ bản của phân thức:
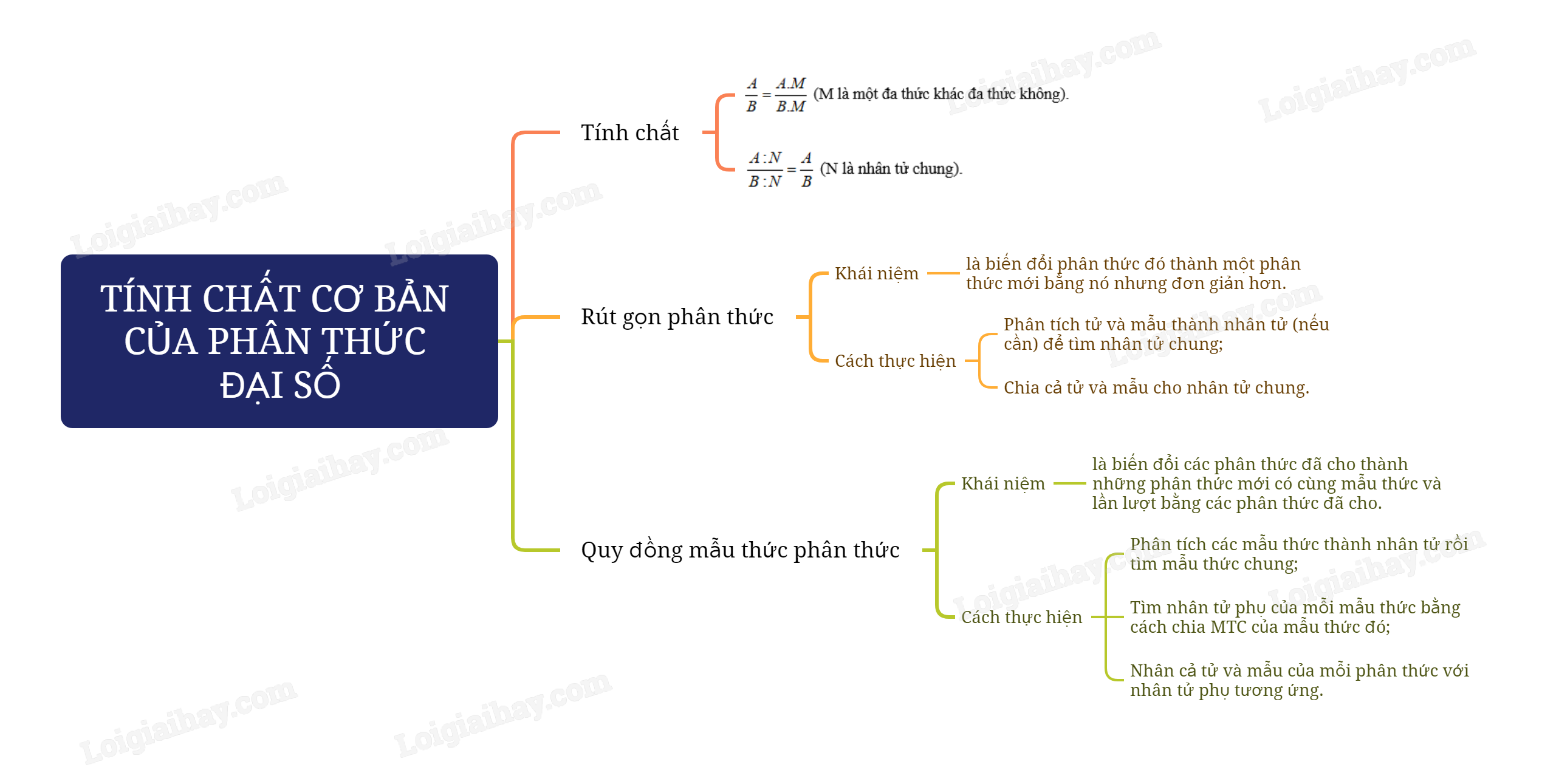
Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
\(\frac{A}{B} = \frac{{A.M}}{{B.M}}\) (M là một đa thức khác đa thức không).
Nếu chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.
\(\frac{{A:N}}{{B:N}} = \frac{A}{B}\) (N là nhân tử chung).
- Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
$\frac{A}{B}=\frac{-A}{-B}$; $\frac{-A}{B}=\frac{A}{-B}=-\frac{A}{B}$.
Ví dụ: Để biến đổi phân thức \(\frac{{x - y}}{{{y^2} - {x^2}}}\) thành \(\frac{{ - 1}}{{x + y}}\), ta chia cả tử và mẫu của phân thức \(\frac{{x - y}}{{{y^2} - {x^2}}}\) cho y – x, khi đó
\(\frac{{x - y}}{{{y^2} - {x^2}}} \\= \frac{{ - (y - x)}}{{(y - x)(y + x)}} \\= \frac{{ - 1}}{{x + y}}\)
2. Rút gọn phân thức
Rút gọn một phân thức là biến đổi phân thức đó thành một phân thức mới bằng nó nhưng đơn giản hơn.
Muốn rút gọn một phân thức đại số ta làm như sau:
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung;
- Chia cả tử và mẫu cho nhân tử chung.
Advertisements (Quảng cáo)
3. Quy đồng mẫu thức nhiều phân thức
Quy đồng mẫu thức nhiều phân thức là biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức và lần lượt bằng các phân thức đã cho.
Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:
- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;
- Tìm nhân tử phụ của mỗi mẫu thức bằng cách chia MTC của mẫu thức đó;
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
Ví dụ: Quy đồng mẫu thức hai phân thức \(\frac{1}{{{x^2} + x}}\) và \(\frac{1}{{{x^2} - x}}\)
MTC là: \(x\left( {x{\rm{ }} + {\rm{ }}1} \right)\left( {x{\rm{ }}-{\rm{ }}1} \right)\)
Ta có:
\(\left[ {x\left( {x{\rm{ }} + {\rm{ }}1} \right)\left( {x{\rm{ }}-{\rm{ }}1} \right)} \right]:\left[ {x(x + 1)} \right] = x - 1;\\\left[ {x\left( {x{\rm{ }} + {\rm{ }}1} \right)\left( {x{\rm{ }}-{\rm{ }}1} \right)} \right]:\left[ {x(x - 1)} \right] = x + 1\)
Khi đó: \(\frac{1}{{{x^2} + x}} = \frac{1}{{x(x + 1)}} = \frac{{x - 1}}{{x(x + 1)(x - 1)}};\\\frac{1}{{{x^2} - x}} = \frac{1}{{x(x - 1)}} = \frac{{x + 1}}{{x(x - 1)(x + 1)}}\)
- Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
$\frac{A}{B}=\frac{-A}{-B}$; $\frac{-A}{B}=\frac{A}{-B}=-\frac{A}{B}$.
