Sử dụng tính chất của hai đường thẳng song song và tính chất của hình thang cân để tính số đo góc. Phân tích và giải Giải bài 2 trang 50 vở thực hành Toán 8 - Luyện tập chung trang 49 . Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết \(\widehat {ABD} = 30^\circ \),
Câu hỏi/bài tập:

Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết \(\widehat {ABD} = 30^\circ \), tính số đo góc của hình thang đó.

Sử dụng tính chất của hai đường thẳng song song và tính chất của hình thang cân để tính số đo góc.
Advertisements (Quảng cáo)

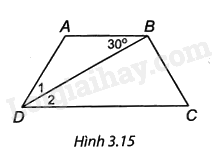
(H.3.15). Tam giác ABD có AB = AD nên ∆ABD cân tại A, do đó \({\widehat D_1} = \widehat {ABD} = 30^\circ .\)
Vì AB // CD nên \({\widehat D_2} = \widehat {ABD} = 30^\circ .\) (hai góc so le trong); suy ra \(\widehat {ADC} = {\widehat D_1} + {\widehat D_2} = 60^\circ .\)
Vì ABCD là hình thang cân nên \(\widehat C = \widehat {ADC} = 60^\circ ,\widehat A = 180^\circ - \widehat {ADC} = 120^\circ = \widehat {ABC}.\)
