Bài 6 trang 118 vở thực hành Toán 8 tập 2: Tính diện tích xung quanh của hình chóp tam giác đều, hình chóp tứ giác đều trong Hình 10...

Tính diện tích xung quanh của hình chóp tam giác đều, hình chóp tứ giác đều trong Hình 10.21

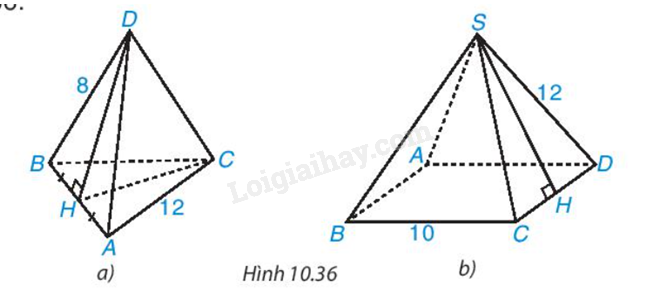
Quan sát hình 10.21: xác định các kích thước và áp dụng công thức tính diện tích xung quanh của hình chóp tam giác, tứ giác đều để tính.

a) BH = 6.

Áp dụng định lý Pythagore cho tam giác DBH vuông tại H, ta có:

$\begin{array}{l}B{H^2} + D{H^2} = B{D^2}\\{6^2} + D{H^2} = {8^2}\\D{H^2} = {8^2} - {6^2}\\DH = 2\sqrt 7 \end{array}$

Diện tích xung quanh của hình chóp D.ABC là:

${S_{xq}} = pd = \frac{{12.3}}{2}.2\sqrt 7 = 36\sqrt 7$.

b) HD = 5.

Áp dụng định lý Pythagore cho tam giác SHD vuông tại H, ta có:

SH² + HD² = SD²

SH² + 52² = 12²

SH² = 12² - 5²

SH = $\sqrt {119}$.

Diện tích xung quanh của hình chóp S.ABCD là:

${S_{xq}} = pd = \frac{{10.4}}{2}.\sqrt {119} = 20\sqrt {119}$.

Quan sát hình 10.21: xác định các kích thước và áp dụng công thức tính diện tích xung quanh của hình chóp tam giác, tứ giác đều để tính.