Câu hỏi/bài tập:

Một người đứng chào cờ (ở vị trí A) cách cột cờ (ở vị trí C) với AC = 20 m. Người đó đặt mắt tại vị trí B cách mặt đất một khoảng là AB = 1,5 m.
Người đó nhìn lên đỉnh cột cờ (ở vị trí E) theo phương BE tạo với phương nằm ngang BD một góc là \(\widehat {EBD} = 32^\circ \) (Hình 20). Tính chiều cao của cột cờ (làm tròn kết quả đến hàng đơn vị của mét).
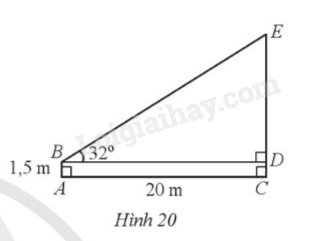

Bước 1: Chứng minh ABDC là hình chữ nhật để suy ra \(AC = BD = 20m,AB = CD = 1,5m\)
Advertisements (Quảng cáo)
Bước 2: Tính ED.
Bước 3: \(EC = DC + ED\).

Xét ABDC có \(\widehat {BAC} = \widehat {ACD} = \widehat {ADC} = 90^\circ \) nên ABDC là hình chữ nhật,
suy ra \(AC = BD = 20m,AB = CD = 1,5m\).
Xét tam giác BED vuông tại B, ta có \(\tan \widehat {EBD} = \frac{{ED}}{{DB}}\) hay \(ED = DB.\tan \widehat {EBD} = 20.\tan 32^\circ \).
Chiều cao cột cờ là \(EC = DC + ED = 1,5 + 20.\tan 32^\circ \approx 14\)m.
