Câu hỏi/bài tập:

Cho nửa đường tròn tâm O đường kính AB. Gọi C, D lần lượt là điểm chính giữa của cung AB, AC.
a) Chứng minh \(\widehat {BAC} = \widehat {COD} = \widehat {ABC} = \widehat {ACO}\).
b) Lấy điểm M thuộc cung CD. Chứng minh \(AM > CM\)và \(\widehat {COM} = 2\widehat {CAM}\).
c) Khi M di chuyển trên cung nhỏ AC, tìm vị trí của điểm M để diện tích của tam giác MAC lớn nhất.

a) Bước 1: Tính số đo các cung CB, CA, CD, AD và từ đó tính được số đo các góc ABC, CAB, COD.
Bước 2: Tính góc ACO (tổng 3 góc trong tam giác ACO).
b) Bước 1: So sánh số đo cung AM và CM, từ đó suy ra \(\widehat {ACM} > \widehat {CAM}\).
Bước 2: Dựa vào mỗi quan hệ giữ góc và cạnh đối diện trong tam giác ACM để so sánh AM, CM.
c) Biểu diễn diện tích tam giác MAC: \(S = \frac{1}{2}AC.MN\)
Ta dự đoán diện tích tam giác MAC khi M là điểm chính giữa của cung AC nên ta chứng minh \(MN \le DK\).

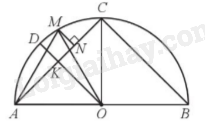
Gọi K là giao điểm của AC và OD, kẻ MN vuông góc với AC tại N.
a) Vì C điểm chính giữa của cung AB nên $\text{sđ}\overset\frown{CB}=\text{sđ}\overset\frown{CA}=\frac{1}{2}\text{sđ}\overset\frown{AB}=\frac{1}{2}.180{}^\circ =90{}^\circ $ (do AB là cung chắn nửa đường tròn nên có số đo là 180⁰),
Advertisements (Quảng cáo)
Suy ra \(\widehat {BAC} = \widehat {ABC} = \frac{{90^\circ }}{2} = 45^\circ \)(do \(\widehat {BAC}\)và \(\widehat {ABC}\)là các góc nội chắn các cung bằng nhau) (1) và \(\widehat {COA} = 90^\circ \)(góc ở tâm chắn cung AC).
Do D là điểm chính giữa của cung AC nên $\text{sđ}\overset\frown{AD}=\text{sđ}\overset\frown{DC}=\frac{1}{2}\text{sđ}\overset\frown{AC}=\frac{1}{2}.90{}^\circ =45{}^\circ $
Suy ra \(\widehat {COD} = 45^\circ \) (do \(\widehat {COD}\) là góc ở tâm chắc cung DC)(2)
Xét tam giác ABC có: \(\widehat {ACO} = 180^\circ - \widehat {CAO} - \widehat {COA} = 180^\circ - 45^\circ - 90^\circ = 45^\circ \) (3)
Từ (1), (2), (3) suy ra \(\widehat {BAC} = \widehat {COD} = \widehat {ABC} = \widehat {ACO}\left( { = 45^\circ } \right)\).
b) Do M thuộc cung nhỏ DC và $\text{sđ}\overset\frown{AD}=\text{sđ}\overset\frown{DC}=45{}^\circ $, mà $\text{sđ}\overset\frown{AM}=\text{sđ}\overset\frown{AD}\text{+sđ}\overset\frown{DM}=45{}^\circ \text{+sđ}\overset\frown{DM}$
Nên $\text{sđ}\overset\frown{AM}>45{}^\circ $ và $\text{sđ}\overset\frown{CM}\text{sđ}\overset\frown{CM}$ hay \(\widehat {ACM} > \widehat {CAM}\)
Xét tam giác ACM có \(\widehat {ACM} > \widehat {CAM}\) nên \(AM > CM\).
Xét (O) có: \(\widehat {CAM}\) là góc nội tiếp chắn cung CM nên $\widehat{CAM}\text{=}\frac{1}{2}\text{sđ}\overset\frown{CM}$; \(\widehat {COM}\) là góc ở tâm chắn cung CM nên $\widehat{COM}\text{=sđ}\overset\frown{CM}$. Do đó \(\widehat {COM} = 2\widehat {CAM}\).
c) Diện tích tam giác MAC là \(S = \frac{1}{2}AC.MN\).
Mà AC cố định nên S lớn nhất khi MN lớn nhất.
Do $\text{sđ}\overset\frown{AD}=\text{sđ}\overset\frown{DC}$ nên \(\widehat {COD} = \widehat {AOD}\) ( do đây là 2 góc ở tâm chắn 2 cung bằng nhau của (O)) nên OD (hay OK) là tia phân giác của góc COA.
Mặt khác \(AO = CO\) (cũng bằng bán kính (O)) nên tam giác ACO cân tại O, do đó đường phân giác OK đồng thời là đường cao, hay \(OK \bot AC\).
Ta lại có \(MN + OK \le OM\)và \(OM = OD = DK + OK\) nên \(MN \le DK\).
Do DK không đổi nên MN lớn nhất khi \(MN = DK\) hay M là điểm chính giữa cung AC.
Vậy diện tích \(\Delta MAC\)lớn nhất bằng \(\frac{1}{2}AC.DK\) khi M là điểm chính giữa cung nhỏ AC.
