Câu hỏi/bài tập:

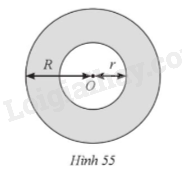
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; R), (O; r) với \(R + r = 1,2dm\), \(R > r\)và diện tích hình vành khuyên đó là 1,5072 dm2 (Hình 55). Tính R và r, \(\pi \approx 3,14\).

Bước 1: Từ \(R + r = 1,2\) suy ra \(R = 1,2 - r\).
Advertisements (Quảng cáo)
Bước 2: Thế \(R = 1,2 - r\) vào \(\pi \left( {{R^2} - {r^2}} \right) = 1,5072\) để tìm r, từ đó tính được R.

Diện tích hình vành khuyên là 1,5072 dm2 nên ta có \(\pi \left( {{R^2} - {r^2}} \right) = 1,5072\) hay \(\left( {R - r} \right)\left( {R + r} \right) = \frac{{1,5072}}{\pi }\) (1)
Mà \(R + r = 1,2\) hay \(R = 1,2 - r\). Thế \(R = 1,2 - r\) vào (1) ta có:
\(\left( {1,2 - r - r} \right)\left( {1,2 - r + r} \right) = \frac{{1,5072}}{\pi }\) nên \(\left( {1,2 - 2r} \right).1,2 = \frac{{1,5072}}{\pi }\), do đó \(1,2 - 2r = \frac{{1,5072}}{{\pi .1,2}}\)
Suy ra \(r \approx 0,4\)dm và \(R = 1,2 - r \approx 1,2 - 0,4 = 0,8\)dm.
