
Cho tam giác OAB vuông tại O. Tính các tỉ số lượng giác của góc A trong mỗi trường hợp sau:
a) AB = 7 cm, OB = 4 cm;
b) OA = 5 cm, OB = 9 cm;
c) AB = 11 cm, OB = 6 cm;

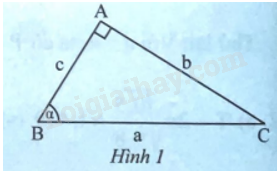
Dựa vào: Tam giác vuông ABC trong Hình 1, ta có:
\(\sin \alpha = \frac{{AC}}{{BC}} = \frac{b}{a};\cos \alpha = \frac{{AB}}{{BC}} = \frac{c}{a};\tan \alpha = \frac{{AC}}{{AB}} = \frac{b}{c};\cot \alpha = \frac{{AB}}{{AC}} = \frac{c}{b}.\)
Chú ý: Với góc nhọn \(\alpha \), ta có:
Advertisements (Quảng cáo)
0
cot \(\alpha \) = \(\frac{1}{{\tan \alpha }}\)

a) \(\sin A = \frac{{OB}}{{AB}} = \frac{4}{7};\cos A = \frac{{OA}}{{AB}} = \frac{{\sqrt {33} }}{7};\)
\(\tan A = \frac{{OB}}{{OA}} = \frac{9}{5};\cot A = \frac{{OA}}{{OB}} = \frac{{\sqrt {33} }}{4}.\)
b) \(\sin A = \frac{{OB}}{{AB}} = \frac{9}{{\sqrt {106} }};\cos A = \frac{{OA}}{{AB}} = \frac{5}{{\sqrt {106} }};\)
\(\tan A = \frac{{OB}}{{OA}} = \frac{9}{5};\cot A = \frac{{OA}}{{OB}} = \frac{5}{9}.\)
c) \(\sin A = \frac{{OB}}{{AB}} = \frac{6}{{11}};\cos A = \frac{{OA}}{{AB}} = \frac{{\sqrt {85} }}{{11}};\)
\(\tan A = \frac{{OB}}{{OA}} = \frac{6}{{\sqrt {85} }};\cot A = \frac{{OA}}{{OB}} = \frac{{\sqrt {85} }}{6}.\)
