Bài 13 trang 74 SBT Toán 9 - Chân trời sáng tạo tập 1: Giải tam giác vuông là tính các cạnh và các góc chưa biết của tam giác đó...

Cho tam giác ABC vuông tại A có đường cao AH, BH = 1 cm, CH = 4 cm. Giải tam giác ABC.

Giải tam giác vuông là tính các cạnh và các góc chưa biết của tam giác đó.

Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.

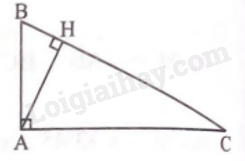
Ta có BC = BH + CH = 1 + 4 = 5 (cm).

Do \(\Delta ABH \backsim \Delta CBA(g.g)\) nên \(\frac{{AB}}{{BH}} = \frac{{BC}}{{AB}}\) hay AB² = BH.BC = 1.5 = 5, suy ra AB = \(\sqrt 5 \) (cm);

Tương tự, ta có \(\Delta CAH \backsim \Delta CBA(g.g)\) nên \(\frac{{AC}}{{BC}} = \frac{{CH}}{{AC}}\) hay AC² = CH. BC = 4. 5 = 20, suy ra \(AC = 2\sqrt 5 (cm)\);

sin C = \(\frac{{AB}}{{BC}} = \frac{{\sqrt 5 }}{5}\), suy ra \(\widehat C \approx {26^o}34’\). Suy ra \(\widehat B \approx {63^o}26’\).