
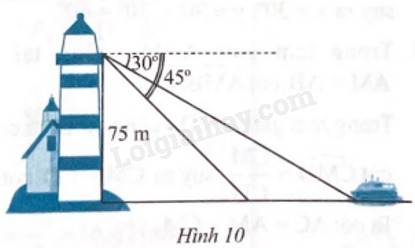
Một người đứng trên một tháp hải đăng ở vị trí cao 75 m so với mặt nước biển đã quan sát hai lần thấy một chiếc thuyền đang hướng về phía tháp hải đăng với góc hạ lần lượt là 30o và 45o (Hình 10). Hỏi thuyền đi được bao nhiêu mét giữa hai lần quan sát?

Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.

Gọi độ cao từ mắt người đó đến mặt nước biển là AB, suy ra AB = 75 m.
Gọi vị trí chiếc thuyền hướng về ngọn hải đăng mà từ trên ngọn tháp quan sát với góc hạ lần lượt là 30o và 45o lần lượt là C, D.
Advertisements (Quảng cáo)
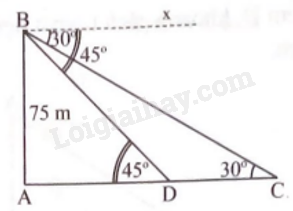
Vì Bx // AD nên \(\left\{ {\begin{array}{*{20}{c}}{\widehat {xBD} = \widehat {BDA} = {{45}^o}}\\{\widehat {xBC} = \widehat {BCA} = {{30}^o}}\end{array}} \right.\) (hai góc so le trong).
Xét \(\Delta ABD\) vuông tại A, ta có \(\widehat {BDA} = {45^o}\), suy ra \(\Delta ABD\) vuông cân tại A.
Suy ra AB = AD = 75 m.
Xét \(\Delta ABC\) vuông tại A, ta có AC = AB. cot \(\widehat {BCA} = 75.\cot {30^o}\), suy ra AC = \(75\sqrt 3 \approx 129,90(m).\)
DC = AC – AD = \(75\sqrt 3 \approx 129,90 - 75 = 54,90(m).\)
Vậy giữa hai lần quan sát, thuyền đi được khoảng 54,90 m.
