Dựa vào công thức chu vi tam giác ABC: \(P = AB + AC + BC;\) diện tích tam giác ABC: \(S = \frac{1}{2}AB. AC\) . Phân tích và lời giải - Bài 17 trang 54 sách bài tập toán 9 - Chân trời sáng tạo tập 1 - Bài tập cuối chương 3. Cho tam giác ABC vuông tại A, (AB = sqrt 2 , AC = sqrt 6 ). Tính giá trị đúng (không làm trò) của a) Chu vi và diện tích tam giác ABC...

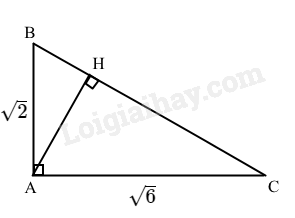
Cho tam giác ABC vuông tại A, \(AB = \sqrt 2 ,AC = \sqrt 6 \). Tính giá trị đúng (không làm trò) của
a) Chu vi và diện tích tam giác ABC.
b) Độ dài đường cao AH của tam giác ABC.

Dựa vào công thức chu vi tam giác ABC: \(P = AB + AC + BC;\)
diện tích tam giác ABC: \(S = \frac{1}{2}AB.AC\) .
Advertisements (Quảng cáo)

a) \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {2 + 6} = \sqrt 8 = 2\sqrt 2 .\)
Chu vi tam giác ABC là:
\(P = AB + AC + BC \\= \sqrt 2 + \sqrt 6 + 2\sqrt 2 = \sqrt 6 + 3\sqrt 2 .\)
Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC = \frac{1}{2}.\sqrt 2 .\sqrt 6 = \sqrt 3 \).
b) Ta có \(S = \frac{1}{2}BC.AH\)
suy ra \(AH = \frac{{2S}}{{BC}} = \frac{{2\sqrt 3 }}{{2\sqrt 2 }} = \frac{{\sqrt 6 }}{2}\).
