Câu 1.1 trang 48 Sách bài tập (SBT) Toán 9 tập 2
Một bể nước hình hộp chữ nhật có đáy hình vuông cạnh bằng x mét. Chiều cao của bể bằng 2m. Kí hiệu V (x) là thể tích của bể.
a) Tính thể tích V(x) theo x.
b) Giả sử chiều cao của bể không đổi, hãy tính V(1), V(2), V(3). Nhận xét khi x tăng lên 2 lần, 3 lần thì thể tích tương ứng của bể tăng lên mấy lần?

Hình hộp chữ nhật đáy hình vuông cạnh x (m) cao 2m.
a) Thể tích của hộp: \(V\left( x \right) = 2{x^2}\)
b) Chiều cao không thay đổi.
\(\eqalign{
& V\left( 1 \right) = {2.1^2} = 2 \cr
& V\left( 2 \right) = 2.{\left( 2 \right)^2} = 8 \cr
& V\left( 3 \right) = 2.{\left( 3 \right)^2} = 18 \cr} \)
Khi cạnh đáy tăng hai lần thì thể tích tăng 4 lần, cạnh đáy tăng lên 3 lần thì thể tích tăng lên 9 lần.
Câu 1.2 trang 48 Sách bài tập (SBT) Toán 9 tập 2
Cho hàm số \(y = f\left( x \right) = a{x^2},a \ne 0.\) Vì sao với hai giá trị đối nhau của x thì hai giá trị tương ứng của hàm số lại bằng nhau?

Hàm số \(y = f\left( x \right) = a{x^2}(a \ne 0)\)
Vì hai giá trị đối nhau của x là x và –x thì \({x^2} = {\left( { - x} \right)^2}\)
\(\Rightarrow f\left( x \right) = f\left( { - x} \right)\)
Vậy hai giá trị đối nhau của x thì giá trị tương ứng của hàm số bằng nhau.
Câu 1.3 trang 48 Sách bài tập (SBT) Toán 9 tập 2
Cho một nửa đường tròn bán kính AB) Điểm M chạy trên nửa đường tròn. Kẻ MH vuông góc với AB tại H. Đặt MH = x.
a) Chứng minh rằng hai tam giác AHM và MHB đồng dạng.
Advertisements (Quảng cáo)
b) Chứng minh rằng \(AH.BH = M{H^2}\).
c) Khi M chuyển động thì x thay đổi, do đó tích AH.BH cũng thay đổi theo. Kí hiệu tích AH.BH bởi P(x). Hỏi P(x) có phải là một hàm số của biến số x hay không? Viết công thức biểu thị hàm số này.

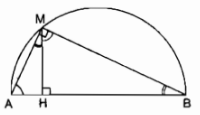
a) ∆ AMB nội tiếp trong đường tròn có AB là đường kính nên \(\widehat {AMB} = 90^\circ \)
Suy ra: \(\widehat {MAB} + \widehat {MBA} = 90^\circ \) (1)
∆ AMH vuông tại H.
\(\widehat {MAH} + \widehat {HMA} = 90^\circ \)
hay \(\widehat {MAB} + \widehat {HMA} = 90^\circ \) (2)
Từ (1) và (2) suy ra: \(\widehat {MBA} = \widehat {HMA}\)
hay \(\widehat {MBH} = \widehat {HMA}\)
Xét ∆ AHM và ∆ MHB:
\(\widehat {AHM} = \widehat {MHB} = 90^\circ \)
\(\widehat {MBH} = \widehat {HMA}\)
Suy ra: ∆ AHM đồng dạng ∆ MHB (g.g)
b) ∆ AHM đồng dạng ∆ MHB
\({{MH} \over {HA}} = {{HB} \over {HM}} \Rightarrow HA.HB = H{M^2}\)
c) Với mỗi giá trị của x ta có một giá trị xác định của P(x).
Vậy P(x) là một hàm số.
\(P(x) = {x^2}\)
