Tính diện tích xung quanh của hình trụ.. Câu 45 trang 174 Sách bài tập (SBT) Toán 9 tập 2 - Bài tập ôn chương IV - Hình trụ - Hình nón - Hình cầu
Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính r = 12cm như hình 112. Hãy tính:
a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.
b) Thể tích hình cầu.
c) Diện tích mặt cầu.
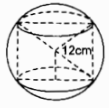
a) Đường chéo mặt cắt hình trụ đi qua trục là đường kính của hình cầu. Hình trụ có đường cao bằng đường kính đáy bằng \(12\sqrt 2 \left( {cm} \right)\)
Advertisements (Quảng cáo)
Diện tích xung quanh hình trụ:
\(\eqalign{
& {S_{xq}} = 2\pi r.h \cr
& {S_{xq}} = \pi .12\sqrt 2 .12\sqrt 2 = 288\pi \left( {c{m^2}} \right) \cr} \)
b) Thể tích hình cầu:
\(V = {4 \over 3}\pi {.12^3} = 2304\left( {c{m^3}} \right)\)
c) Diện tích mặt cầu:
\(S = 4\pi {.12^2} = 576\pi \left( {c{m^3}} \right)\)