Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O’) có đường kính CB.
a) Hai đường tròn (O) và (O’) có vị trí tương đối như thế nào đối với nhau ?
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì ? Vì sao?
c) Gọi K là giao điểm của DB và đường tròn (O’). Chứng minh rằng ba điểm E, C, K thẳng hàng.
d) Chứng minh rằng HK là tiếp tuyến của đường tròn (O’).

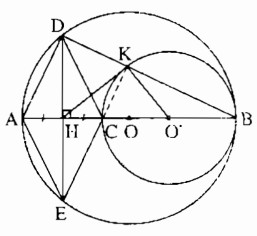
a) Vì O, O’ và B thẳng hàng nên: O’B < OB ⇒ O’ nằm giữa O và B
Ta có: OO’ = OB - O¢B
Vậy đường tròn (O’) tiếp xúc với đường tròn (O) tại B.
b) Ta có: HA = HC (gt)
AB ⊥ DE (gt)
Suy ra: HD = HE (đường kính vuông góc với dây cung)
Tứ giác ADCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: AC ⊥ DE
Suy ra tứ giác ADCE là hình thoi.
c) Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại D.
Suy ra: AD ⊥ BD
Advertisements (Quảng cáo)
Tứ giác ADCE là hình thoi nên EC // AD
Suy ra: EC ⊥ BD (1)
Tam giác BCK nội tiếp trong đường tròn (O¢) có BC là đường kính nên vuông tại K.
Suy ra: CK ⊥ BD (2)
Từ (1) và (2) suy ra EC trùng với CK
Vậy E, C, K thẳng hàng.
d) Tam giác DEK vuông tại K có KH là trung tuyến thuộc cạnh huyền DE nên:
\(HK = HE = {1 \over 2}DE\) (tính chất tam giác vuông)
Suy ra tam giác EHK cân tại H
Suy ra: \(\widehat {HEK} = \widehat {HKE}\) (tính chất tam giác cân) (3)
Ta có: O’K = O’C (= R) nên tam giác O’CK cân tại O’
Suy ra: \(\widehat {O’KC} = \widehat {O’CK}\) (tính chất tam giác cân)
Mà: \(\widehat {O’CK} = \widehat {HCE}\) (đối đỉnh)
Suy ra: \(\widehat {O’KC} = \widehat {HCE}\) (4)
Từ (3) và (4) suy ra: \(\widehat {HKO’} = \widehat {HKE} + \widehat {O’KC} = \widehat {HEK} + \widehat {HCE}\) (5)
Tam giác CEH vuông tại H nên \(\widehat {HEK} + \widehat {HCE} = 90^\circ \) (6)
Từ (5) và (6) suy ra: \(\widehat {HKO’} = 90^\circ \) hay HK ⊥ KO’ tại K
Vậy HK là tiếp tuyến của đường tròn (O’).
