Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB.
a) Chứng minh rằng ba điểm M, H, O thẳng hàng.
b) Tứ giác AOBH là hình gì ?
c) Khi M di chuyển trên xy thì H di chuyển trên đường nào ?

Advertisements (Quảng cáo)
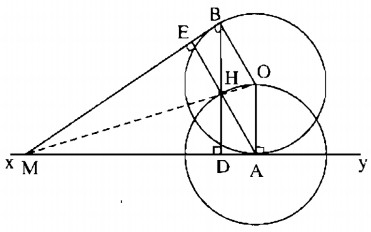
a) Gọi BD, AE là các đường cao của ∆MAB. Ta có ∆MAE = ∆MBD ( cạnh huyền – góc nhọn) nên ME = MD, ∆MHE = ∆MHD ( cạnh huyền – cạnh góc vuông) nên \(\widehat {EMH} = \widehat {DMH}\). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
b) Tứ giác AOBH có BH // OA, AH // OB và OA = OB nên là hình thoi.
c) H cách A cố định một khoảng bằng OA không đổi nên H di chuyển trên đường tròn (A ; AO).
