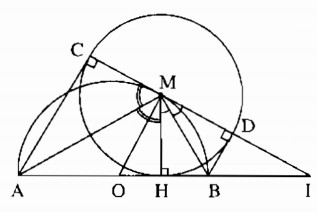
Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tròn (M ; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M ( C và D là các tiếp điểm khác H).
a) Chứng minh rằng ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của đường tròn (O).
b) Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi.
c) Giả sử CD và AB cắt nhau tại I. Chứng minh rằng tích OH.OI không đổi.

a) Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
− MA là tia phân cách của góc HMC
Suy ra: \(\widehat {CMA} = \widehat {HMA}\) hay \(\widehat {CMH} = 2\widehat {HMA}\)
− MB là tia phân giác của góc HMD
Suy ra: \(\widehat {HMB} = \widehat {DMB}\) hay \(\widehat {DMH} = 2\widehat {HMB}\)
Tam giác ABM nội tiếp đường tròn (O) có AB là đường kính nên vuông tại M
Suy ra: \(\widehat {AMB} = 90^\circ \) hay \(\widehat {HMA} + \widehat {HMB} = 90^\circ \)
Suy ra: \(\widehat {CMH} + \widehat {HMD} = 2\widehat {HMA} + 2\widehat {HMB}\)
\(= 2 (\widehat {HMA} + \widehat {HMB}) = 2.90^\circ = 180^\circ \)
Advertisements (Quảng cáo)
Vậy C, M, D thẳng hàng.
b) Trong đường tròn (M ; MH), theo (tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH.
Suy ra: AC + BD = AH + BH = AB không đổi
c) Ta có: AC ⊥ CD và BD ⊥ CD ( tính chất tiếp tuyến)
Suy ra: AC // BD hay tứ giác ABDC là hình thang
Mà OA = OB ( bán kính (O))
Và AC = MD ( bán kính (M))
Suy ra OM là đường trung bình của hình thang ABCD
Khi đó OM // AC. Suy ra: OM ⊥ CD hay \(\widehat {OMI} = 90^\circ \)
Tam giác OMI vuông tại M có MH ⊥ OI.
Theo hệ thức lượng trong tam giác vuông, ta có:
OM2 = OH.OI
Suy ra: OH.OI = R2 không đổi.
