
Trong Hình 92, cho các điểm \(A,B,C,D,E\) thuộc đường tròn \(\left( O \right)\).
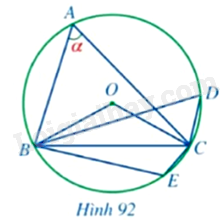
a) Số đo góc \(BOC\) là:
A. \(\alpha \)
B. \(2\alpha \)
C. \(180^\circ - \alpha \)
B. \(180^\circ - 2\alpha \)
b) Số đo góc \(BDC\) là:
A. \(\alpha \)
B. \(\frac{\alpha }{2}\)
C. \(180^\circ - \alpha \)
D. \(180^\circ - \frac{\alpha }{2}\)
c) Số đo góc \(BEC\) là:
Advertisements (Quảng cáo)
A. \(\alpha \)
B. \(2\alpha \)
C. \(180^\circ - \alpha \)
D. \(360^\circ - \alpha \)

Dựa vào mối liên hệ giữa góc nội tiếp đường tròn và góc ở tâm để tính.

a) Do \(\widehat {BOC}\) là góc ở tâm chắn cung $\overset\frown{BC}$, \(\widehat {BAC}\) là góc nội tiếp chắn cung $\overset\frown{BC}$ nên \(\widehat {BOC} = 2\widehat {BAC} = 2\alpha \).
Chọn đáp án B.
b) Do \(\widehat {BDC}\) là góc nội tiếp chắn cung $\overset\frown{BC}$, \(\widehat {BAC}\) là góc nội tiếp chắn cung $\overset\frown{BC}$ nên \(\widehat {BAC} = \widehat {BDC} = \alpha \).
Chọn đáp án A.
c) Do \(\widehat {BEC}\) là góc nội tiếp chắn cung lớn $\overset\frown{BC}$, \(\widehat {BAC}\) là góc nội tiếp chắn cung nhỏ $\overset\frown{BC}$ nên \(\widehat {BEC} = \frac{1}{2}\left( {360^\circ - 2\alpha } \right) = 180^\circ - \alpha \).
Chọn đáp án C.
