
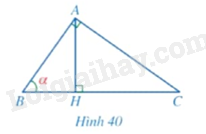
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha \) (Hình 40).
a) Tỉ số \(\frac{{HA}}{{HB}}\) bằng:
A. \(\sin \alpha \).
B. \(\cos \alpha \).
C. \(\tan \alpha \).
D. \(\cot \alpha \).
b) Tỉ số \(\frac{{HA}}{{HC}}\) bằng:
A. \(\sin \alpha \).
B. \(\cos \alpha \).
C. \(\tan \alpha \).
D. \(\cot \alpha \).
c) Tỉ số \(\frac{{HA}}{{AC}}\) bằng:
A. \(\sin \alpha \).
B. \(\cos \alpha \).
Advertisements (Quảng cáo)
C. \(\tan \alpha \).
D. \(\cot \alpha \).

Dựa vào tỉ số lượng giác để giải bài toán.

a) Chọn đáp án C.
b) Xét tam giác \(AHC\) vuông tại \(H\) có:
\(\tan C = \frac{{HA}}{{HC}}\).
Do \(\widehat B + \widehat C = 90^\circ \) nên \(\tan C = \cot B\).
Vậy \(\cot \alpha = \frac{{HA}}{{HC}}\).
Chọn đáp án D.
c) Xét tam giác \(AHC\) vuông tại \(H\) có:
\(\sin C = \frac{{HA}}{{AC}}\).
Do \(\widehat B + \widehat C = 90^\circ \) nên \(\sin C = \cos B\).
Vậy \(\cos \alpha = \frac{{HA}}{{AC}}\).
Chọn đáp án B.
