
Cho đường tròn \(\left( {O;R} \right)\) và dây \(AB\) sao cho \(\widehat {AOB} = 90^\circ \). Giả sử \(M,N\) lần lượt là các điểm thuộc cung lớn \(AB\) và cung nhỏ \(AB\) (\(M,N\) khác \(A\) và \(B\)).
a) Tính độ dài đoạn thẳng \(AB\) theo \(R\).
b) Tính số đo các góc \(ANB\) và \(AMB\).

Dựa vào tính chất góc ở tâm và góc nội tiếp để tính.

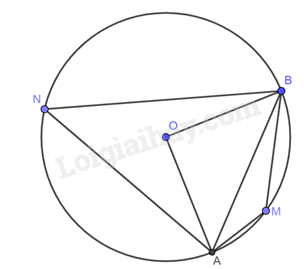
a) Áp dụng định lí Pythagore vào tam giác \(AOB\) vuông tại \(O\), ta có:
Advertisements (Quảng cáo)
\(O{A^2} + O{B^2} = A{B^2} \Rightarrow A{B^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow AB = \sqrt 2 R\)
b) Xét đường tròn \(\left( O \right)\):
+) Vì \(\widehat {ANB}\) là góc nội tiếp và \(\widehat {AOB}\) là góc ở tâm cùng chắn cung \(AB\) nên:
\(\widehat {ANB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.90^\circ = 45^\circ \).
+) $sđ\overset\frown{AMB}=360{}^\circ -sđ\overset\frown{ANB}=360{}^\circ -90{}^\circ =270{}^\circ $
+) Vì \(\widehat {AMB}\) là góc nội tiếp chắn cung \(AMB\) nên:
$\widehat{AMB}=\frac{1}{2}sđ\overset\frown{AMB}=\frac{1}{2}.270{}^\circ =135{}^\circ $.
Vậy \(\widehat {ANB} = 45^\circ ,\widehat {AMB} = 135^\circ \).
