Dựa vào tính chất tiếp tuyến để chứng minh.. Lời giải bài tập, câu hỏi bài tập 3 trang 110 SGK Toán 9 tập 1 - Cánh diều Bài 3. Tiếp tuyến của đường tròn. Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng thẳng \(c, d\) đi qua \(M\) lần lượt tiếp xúc với \(\left( O \right)\) tại \(A, B\)...
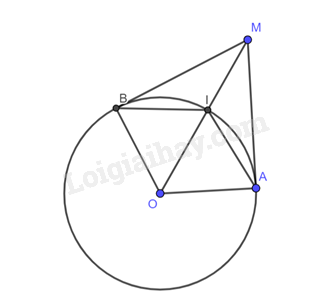
Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng thẳng \(c,d\) đi qua \(M\) lần lượt tiếp xúc với \(\left( O \right)\) tại \(A,B\). Tia phân giác của góc \(MAB\) cắt \(MO\) tại \(I\). Chứng minh điểm \(I\) cách đều ba đường thẳng \(MA,MB\) và \(AB\).
Dựa vào tính chất tiếp tuyến để chứng minh.
Advertisements (Quảng cáo)
Do \(MA,MB\) là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(MO\) là tia phân giác của \(\widehat {AMB}\) hay \(MI\) là tia phân giác của \(\widehat {AMB}\).
Xét tam giác \(AMB\) có:
\(BI\) là tia phân giác của góc \(MAB\);
\(MI\) là tia phân giác của góc \(AMB\).
Suy ra \(I\) là giao điểm của 3 đường phân giác tam giác \(AMB\).
Vậy \(I\) cách đều \(MA,MB,AB\).