
Cho bán kính đường tròn nội tiếp tam giác đều bằng 4cm. Tính cạnh của tam giác đều đó.

Bước 1: Áp dụng tính chất đường trung tuyến của tam giác để tính EI.
Bước 2: Biểu diễn FI theo FG và EF.
Bước 3: Áp dụng định lý Pytago trong tam giác EFI để tính cạnh EF.

Advertisements (Quảng cáo)
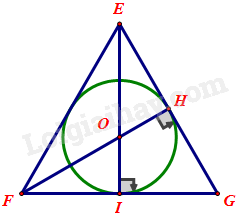
Gọi (O; OI) là đường tròn nội tiếp tam giác đều EFG nên O là giao của đường trung trực EI, FH; và OI = 4cm.
EI là đường trung trực của tam giác đều EFG nên \(FI = \frac{{FG}}{2} = \frac{{EF}}{2}\) và EI đồng thời là đường trung tuyến do đó \(EI = 3OI = 3.4 = 12cm.\)
Áp dụng định lý Pytago trong tam giác EFI vuông tại I:
\(\begin{array}{l}E{F^2} = E{I^2} + F{I^2}\\E{F^2} = {12^2} + {\frac{{EF}}{4}^2}\\\frac{{3E{F^2}}}{4} = 144\\EF = 8\sqrt 3 cm.\end{array}\)
Vậy cạnh của tam giác đều là \(8\sqrt 3 cm.\)
