
Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3 dm, 5 dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm.

Bước 1: Áp dụng Định lý Pytago trong tam giác vuông ACB để tính đường kính AC.
Bước 2: Áp dụng công thức \(S = \pi .\frac{{{d^2}}}{4}.\)

Advertisements (Quảng cáo)
Mặt trên của tấm nệm được biểu diễn bằng hình học như sau:
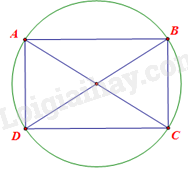
Hình chữ nhật ABCD có chiều dài AB = 5 dm, chiều rộng BC = 3 dm.
Xét tam giác ACB vuông tại B có:
\(\begin{array}{l}A{B^2} + B{C^2} = A{C^2}(Pytago)\\{5^2} + {3^2} = A{C^2}\\AC = \sqrt {34} dm\end{array}\)
Mà hình chữ nhật ABCD nội tiếp đường tròn nên đường kính tấm đệm là\(AB = \sqrt {34} dm.\)
Diện tích hình tròn là: \(S = \pi .\frac{{{d^2}}}{4} = \pi .\frac{{{{\sqrt {34} }^2}}}{4} = \frac{{17\pi }}{2}d{m^2}.\)
