
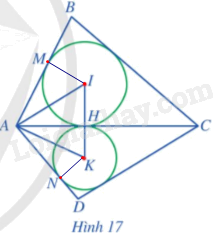
Cho tứ giác ABCD có các tam giác ABC và ACD lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17). Chứng minh:
a) Ba điểm I, H, K thẳng hàng.
b) AM = AN.
c) \(\widehat {IAK} = \frac{1}{2}\widehat {BAD}.\)

a) Chứng minh \(\widehat {IHA} + \widehat {AHK} = \widehat {IHK} = 90^\circ + 90^\circ = 180^\circ \).
b) Chứng minh \(\Delta IMA = \Delta IHA(g.c.g)\) và \(\Delta KHA = \Delta KNA(g.c.g)\) suy ra AM = AN ( = AH).
c) Từ 2 cặp tam giác bằng nhau ở câu b ta suy ra được \(\widehat {HAI + }\widehat {HAK} = \frac{1}{2}\widehat {MAN}\), từ đó ta có điều phải chứng minh.

a) Do đường tròn (I) nội tiếp tam giác ABC và tiếp xúc với đường thẳng AC tại H nên \(IH \bot AC\), suy ra \(\widehat {IHA} = 90^\circ .\)
Do đường tròn (K) nội tiếp tam giác ADC và tiếp xúc với đường thẳng AC tại H nên \(KH \bot AC\), suy ra \(\widehat {IHK} = 90^\circ .\)
Ta có: \(\widehat {IHA} + \widehat {AHK} = \widehat {IHK} = 90^\circ + 90^\circ = 180^\circ \), nên I, H, K thẳng hàng.
b) Ta có: Đường tròn (I) nội tiếp tam giác ABC nên IH = IM, và \(IM \bot AB\) hay \(\widehat {IMA} = 90^\circ .\)
Xét tam giác IMA và tam giác IHA có:
AI chung
IM = IH (cmt)
Advertisements (Quảng cáo)
\(\widehat {IMA} = \widehat {IHA} = 90^\circ \)
Suy ra \(\Delta IMA = \Delta IHA(g.c.g)\)
Do đó AM = AH (2 cạnh tương ứng) (i)
Ta có: Đường tròn (K) nội tiếp tam giác ADC nên KH = KN, và \(NK \bot AD\) hay \(\widehat {KNA} = 90^\circ .\)
Xét tam giác KHA và tam giác KNA có:
AK chung
KH = KN (cmt)
\(\widehat {KHA} = \widehat {KNA} = 90^\circ \)
Suy ra \(\Delta KHA = \Delta KNA(g.c.g)\)
Do đó AN = AH (2 cạnh tương ứng) (ii)
Từ (i) và (ii) suy ra AM = AN ( = AH).
c) Từ câu b ta có:
\(\Delta IMA = \Delta IHA\) nên \(\widehat {MAI} = \widehat {HAI}\) (hai góc tương ứng)
\(\Delta KHA = \Delta KNA\) nên \(\widehat {HAK} = \widehat {KAN}\)(hai góc tương ứng)
Mà \(\widehat {MAI} + \widehat {HAI + }\widehat {HAK} + \widehat {KAN} = \widehat {MAN}\)
Nên \(2\widehat {HAI + }2\widehat {HAK} = \widehat {MAN}\) do đó \(\widehat {HAI + }\widehat {HAK} = \frac{1}{2}\widehat {MAN}\)
Hay \(\widehat {IAK} = \frac{1}{2}\widehat {BAD}.\)
