Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 68
Cho biết các đỉnh của tam giác ABC (Hình 2) có thuộc đường tròn (O) hay không?
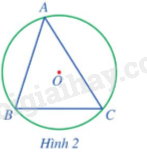

Kiểm tra xem 3 đỉnh của tam giác có nằm trên đường tròn hay không.

Ta thấy 3 đỉnh A, B, C của tam giác ABC đều thuộc đường tròn tâm (O).
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 69
Quan sát Hình 4 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tam giác ABC, đường tròn nào ngoại tiếp tam giác ABD?
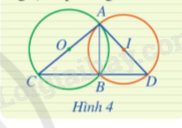

Kiểm tra từng đường tròn để biết các điểm thuộc đường tròn đó là đỉnh của tam giác nào.

Đường tròn (O) là đường tròn ngoại tiếp tam giác ABC vì nó đi qua cả 3 đỉnh A, B, C của tam giác ABC.
Đường tròn (I) là đường tròn ngoại tiếp tam giác ABD vì nó đi qua cả 3 đỉnh A, B, C của tam giác ABD.
Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 69
Cho tam giác ABC có O là giao điểm của ba đường trung trực (Hình 5).
a) Các đoạn thẳng OA, OB, OC có bằng nhau không?
b) Đặt R = OA. Đường tròn (O;R) có phải là đường tròn ngoại tiếp tam giác ABC hay không? Vì sao?
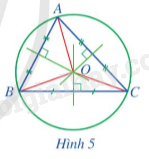

a) Nhớ lại tính chất 3 đường trung trực của tam giác.
b) Chỉ ra OA = OB = OC = R.

a) Do 3 đường trung trực của tam giác ABC cắt nhau tại 1 điểm nên OA = OB = OC (tính chất 3 đường trung trực trong tam giác).
b) Ta có R = OA nên OA = OB = OC = R.
Vậy đường tròn (O; R) là đường tròn ngoại tiếp tam giác ABC.
Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 70
Cho tam giác ABC vuông tại A. Gọi O là trung điểm của BC (hình 7). Đường tròn (O; OB) có phải là đường tròn ngoại tiếp tam giác ABC hay không?
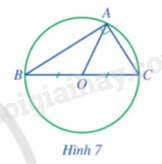

Áp dụng định lí “Đường trung tuyến ứng với cạnh huyền trong tam giác vuông bằng một nửa cạnh huyền”.

Vì O là trung điểm của BC nên AO là đường trung tuyến của tam giác ABC.
Xét tam giác ABC vuông tại A có AO là đường trung tuyến ứng với cạnh huyền BC nên ta có: \(OA = OB = OC = \frac{{BC}}{2}\)
Vậy 3 điểm A, B, C thuộc đường tròn đường kính OB nên (O; OB) là đường tròn ngoại tiếp tam giác ABC.
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 70
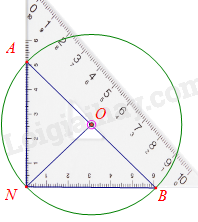
Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó.

Áp dụng định lí “Đường trung tuyến ứng với cạnh huyền trong tam giác vuông bằng một nửa cạnh huyền”.
Advertisements (Quảng cáo)
Tâm đường tròn ngoại tiếp tam giác vuông chính là trung điểm của cạnh huyền.

Đặt đỉnh vuông của eke trùng với một điểm N bất kỳ trên đường tròn, kẻ đường thẳng đi qua cạnh huyền của êke cắt đường tròn tại A và B ta được đường kính AB.
Trung điểm của AB là tâm của đường tròn đó.
Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 70
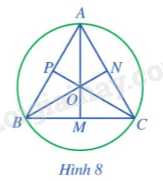
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 8).
a) AM, BN, CP có là các đường trung trực của tam giác ABC hay không?
b) Điểm O có là tâm đường tròn ngoại tiếp tam giác ABC hay không?
c) Tính AM theo a.
d) Tính OA theo a.

a) Nhớ lại tính chất: Đường trung tuyến xuất phát từ đỉnh của tam giác cân cũng là đường trung trực của tam giác đó.
b) Xét xem O có cách đều 3 đỉnh của tam giác hay không.
c) Tính BM, sau đó áp dụng định lý Pytago trong tam giác vuông AMB.
d) Áp dụng: khoảng cách từ trọng tâm tới đỉnh của tam giác bằng \(\frac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.

a) Vì tam giác ABC đều nên ba đường trung tuyến AM, BN, CP cũng đồng thời là ba đường trung trực của tam giác ABC. Do đó AM, BN, CP lần lượt là trung trực của BC, AC, AB.
b) Do ba đường trung trực của tam giác ABC cắt nhau tại O nên O cách đều 3 đỉnh A, B, C (tính chất 3 đường trung trực của tam giác).
Vậy O là tâm đường tròn ngoại tiếp tam giác ABC.
c) Xét tam giác đều ABC cạnh a có trung tuyến AM nên \(BM = \frac{1}{2}BC = \frac{a}{2}.\)
AM là đường trung trực của tam giác ABC (cmt) nên \(AM \bot BC\) do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác ABM vuông tại M có:
\(A{M^2} = A{B^2} - B{M^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\) (Pytago)
\(AM = \frac{{\sqrt 3 a}}{2}.\)
d) Ta có: AM là trung tuyến của tam giác ABC, O là trọng tâm nên \(OA = \frac{2}{3}AM = \frac{2}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{3}.\)
Luyện tập3
Trả lời câu hỏi Luyện tập 3 trang 71
Cho tam giác đều ABC nội tiếp đường tròn (O; 2cm). Tính AB.

Kẻ đường trung trực AH.
Áp dụng Định lý độ dài đường trung tuyến trong tam giác để tính AH.
Áp dụng Định lý Pytago để tính BH rồi tính AB.

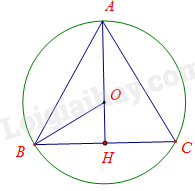
Chứng minh
Kẻ đường trung trực AH của tam giác ABC suy ra \(O \in AH,\widehat {OHB} = 90^\circ .\)
Vì tam giác đều ABC nội tiếp đường tròn (O; 2cm) nên OA = OB = 2cm.
Ta lại có: AH là đường trung trực của tam giác đều ABC nên AH đồng thời là đường trung tuyến, do đó \(OH = \frac{1}{2}AO = \frac{1}{2}.2 = 1cm,AH = 3OH = 3.1 = 3cm.\)
Xét tam giác OHB vuông tại H, áp dụng định lý Pytago ta có: \(BH = \sqrt {B{O^2} - O{H^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 cm.\)
Xét tam giác AHB vuông tại H, áp dụng định lý Pytago ta có:
\(AB = \sqrt {{3^2} + {{\sqrt 3 }^2}} = 2\sqrt 3 cm.\)
Vậy\(AB = 2\sqrt 3 cm.\)
