Hoạt động5
Trả lời câu hỏi Hoạt động 5 trang 71
Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).
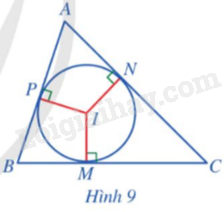

Các vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I) gồm: cắt nhau tại 2 điểm, tiếp xúc nhau (cắt nhau tại 1 điểm), không cắt nhau.

Các đường thẳng AB, BC, CA tiếp xúc với đường tròn (I) lần lượt tại các điểm: P, M, N.
Luyện tập4
Trả lời câu hỏi Luyện tập 4 trang 72
Trong Hình 11, đường tròn (I) là đường tròn nội tiếp những tam giác nào?

Xác định (I) tiếp xúc với các cạnh thuộc tam giác nào.

Đường tròn (I) là đường tròn nội tiếp tam giác ABC vì nó tiếp xúc với ba cạnh AB, BC, CA.
Đường tròn (I) là đường tròn nội tiếp tam giác BDE vì nó tiếp xúc với ba cạnh DE, DC, EC.
Hoạt động6
Trả lời câu hỏi Hoạt động 6 trang 72
Cho tam giác ABC có I là giao điểm của ba đường phân giác. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hình 12).
a) So sánh các đoạn thẳng IM, IN, IP.
b) Đặt r = IM. Đường tròn (I; r) có phải là đường tròn nội tiếp tam giác ABC hay không? Vì sao?
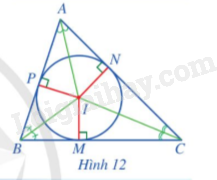

a) Áp dụng tính chất 3 đường phân giác trong tam giác.
b) Chứng minh IM = IN = IP = r.

a) Do I là giao của 3 đường phân giác trong tam giác ABC nên I cách đều 3 cạnh của tam giác, do đó IM = IN = IP.
b) Vì r = IM, mà IM = IN = IP nên IM = IN = IP = r.
Vậy đường tròn (I; r) là đường tròn nội tiếp tam giác ABC
Hoạt động7
Trả lời câu hỏi Hoạt động 7 trang 73
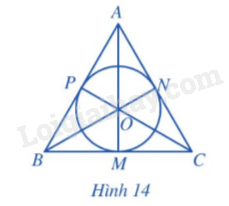
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 14).
a) AM, BN, CP có là các đường phân giác của tam giác ABC hay không?
Advertisements (Quảng cáo)
b) Điểm O có là tâm đường tròn nội tiếp tam giác ABC hay không?
c) Tính OM theo a.

a) Áp dụng: Trong tam giác cân, đường trung tuyến đồng thời là đường phân giác.
b) Chứng minh OM = ON = OP.
c) Áp dụng Pytago trong tam giác AMB vuông tại M.

a) Vì tam giác ABC đều nên ba đường trung tuyến AM, BN, CP đồng thời là ba đường phân giác.
b) Do O là giao của 3 đường phân giác trong tam giác ABC nên O cách đều 3 cạnh của tam giác, do đó OM = ON = OP.
Vậy đường tròn (O) là đường tròn nội tiếp tam giác ABC.
c) Xét tam giác ABC đều có đường trung tuyến AM nên \(BM = \frac{{BC}}{2} = \frac{a}{2}\) và AM đồng thời là đường cao, do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác AMB vuông tại M có:
\(AM = \sqrt {A{B^2} - B{M^2}} \) (Pytago).
Nên \(AM = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{\sqrt 3 a}}{2}.\)
Mà \(OM = \frac{1}{3}AM\)(do AM là đường trung tuyến trong tam giác ABC).
Suy ra \(OM = \frac{1}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{6}.\)
Luyện tập5
Trả lời câu hỏi Luyện tập 5 trang 73
Cho tam giác đều ABC ngoại tiếp đường tròn (O; 6). Tính AB.

Bước 1: Tính AM (dựa vào tính chất đường trung tuyến trong tam giác).
Bước 2: Tính BM theo AB.
Bước 3: Áp dụng Định lý Pytago trong tam giác vuông AMB.

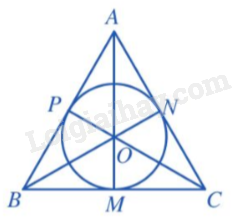
Giả sử tam giác ABC ngoại tiếp (O) với phân giác AM, suy ra AM đồng thời là đường trung tuyến.
Có đường tròn (O; 6) nên OM = 6.
Xét tam giác ABC đều có đường trung tuyến AM nên \(AM = 3OM = 3.6 = 18\) và \(BM = \frac{{BC}}{2} = \frac{{AB}}{2}\), đồng thời AM cũng là đường cao, do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác AMB vuông tại M có:
\(\begin{array}{l}A{M^2} + B{M^2} = A{B^2}(Pytago)\\A{M^2} + {\frac{{AB}}{4}^2} = A{B^2}\\{18^2} = {\frac{{3AB}}{4}^2}\\AB = 12\sqrt 3 \end{array}\)
Vậy \(AB = 12\sqrt 3 .\)
