Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 95
Cho đường tròn \(\left( {O;R} \right)\)
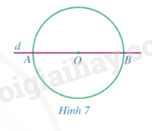
a) Vẽ đường thẳng \(d\) đi qua tâm \(O\) cắt đường tròn tại \(A,B\). So sánh \(OA\) và \(OB\) (Hình 7).
b) Giả sử \(M\) là một điểm tùy ý trên đường tròn \(\left( {O;R} \right)\). Trên tia đối của tia \(OM\), ta lấy điểm \(N\) sao cho \(ON = OM\). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?

Dựa vào hình ảnh trực quan để trả lời bài toán.

a) \(OA = OB = R\).
b) Do \(OM = R\) lại có \(ON = OM\) nên \(ON = R\). Vậy \(N\) thuộc đường tròn \(\left( {O;R} \right)\).
Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 95
Cho đường tròn \(\left( {O;R} \right)\). Giả sử \(d\) là đường thẳng đi qua tâm \(O\) và \(M\) là một điểm tùy ý trên đường tròn \(\left( {O;R} \right)\). Kẻ \(MH \bot d\left( {H \in d} \right)\). Trên tia \(MH\) lấy điểm \(N\) sao cho \(H\) là trung điểm của \(MN\) (ta gọi điểm \(N\) là điểm đối xứng với điểm \(M\) qua đường thẳng \(d\)). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
Advertisements (Quảng cáo)

Dựa vào kiến thức vừa học để trả lời câu hỏi.

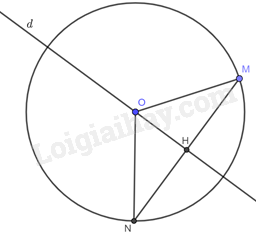
Do \(OH \bot MN\), \(MH = HN\) nên \(OH\) là đường trung trực của \(MN\). Vậy \(OM = ON\).
Lại có \(OM = R\) nên \(ON = R\). Vậy \(N\) có thuộc đường tròn \(\left( {O;R} \right)\).
Luyện tập3
Trả lời câu hỏi Luyện tập 3 trang 96
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm đường tròn đó.

Dựa vào đường tròn là hình có trục đối xứng để gấp.

Ta gấp tờ giấy làm đôi sau đó gấp đôi thêm một lần nữa. Giao điểm của hai lần gấp chính là tâm của đường tròn.
