Tính \(\widehat {CMB}\) bằng cách dựa vào tính chất trong một tứ giác tổng các góc bằng 360o. Lời giải bài tập, câu hỏi bài tập 1 trang 88 SGK Toán 9 tập 1 - Chân trời sáng tạo Bài 2. Tiếp tuyến của đường tròn. Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; \(\widehat {COB} = {130^o}\). Tính số đo \(\widehat {CMB}\)...

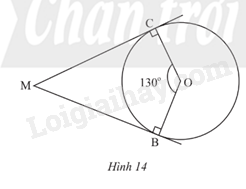
Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; \(\widehat {COB} = {130^o}\). Tính số đo \(\widehat {CMB}\) .

Advertisements (Quảng cáo)
Tính \(\widehat {CMB}\) bằng cách dựa vào tính chất trong một tứ giác tổng các góc bằng 360o.

Xét tứ giác MBOC ta có:
\(\begin{array}{l}\widehat {CMB} = {360^o} - (\widehat {MCO} + \widehat {MBO} + \widehat {COB})\\ = {360^o} - (2\widehat {MCO} + \widehat {COB})\\ = {360^o} - ({2.90^o} + {130^o})\\ = {50^o}\end{array}\)
