Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 85
Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A).
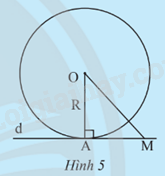
a) Giải thích tại sao ta có OA = R và OM > R.
b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.

- Dựa vào khoảng cách từ tâm đến một điểm trên đường tròn thì bằng bán kính.
- Dựa vào tính chất: Trong tam giác vuông, cạnh huyền (đối diện cạnh góc vuông) là cạnh lớn nhất.
- Dựa vào định nghĩa: Có duy nhất một điểm chung C khi đường thẳng a tiếp xúc (O) tại C, khi đó a là tiếp tuyến của đường tròn (O) và C là tiếp điểm.

a) Ta có OA = R vì điểm O nằm trên đường tròn (O; R).
Xét tam giác AOM vuông tại A ta có AM và OA là cạnh góc vuông, OM là cạnh huyền nên OM > OA mà R = OA suy ra OM > R.
b) d và (O) không thể có điểm chung nào khác ngoài A vì d tiếp xúc với (O) và d là tiếp tuyến của (O).
Thực hành2
Advertisements (Quảng cáo)
Trả lời câu hỏi Thực hành 2 trang 86
Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H.
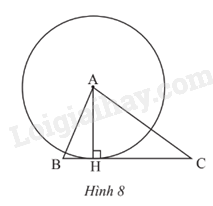

Dựa vào dấu hiệu nhận biết của đường tròn: Một đường thẳng là tiếp tuyến của đường tròn khi nó đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.

Ta có BC là tiếp tuyến của đường tròn (A; AH) vì BC đi qua điểm H thuộc đường tròn (A; AH) và BC vuông góc với AH.
Vận dụng2
Trả lời câu hỏi Vận dụng 2 trang 86
Một diễn viên xiếc đi xe đạp trên một sợi dây cáp căng (Hình 9). Ta coi sợi dây là tiếp tuyến của mỗi bánh xe, xác định các tiếp điểm.
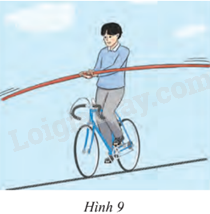

Dựa vào định nghĩa: Có duy nhất một điểm chung C khi đường thẳng a tiếp xúc (O) tại C, khi đó a là tiếp tuyến của đường tròn (O) và C là tiếp điểm.

Tiếp điểm là giao điểm tiếp xúc của nan hoa với dây cáp.
