
Cho tam giác ABC có đương tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm; BP = 3 cm; CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.
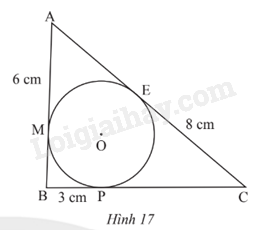

- Dựa vào tính chất hai tiếp tuyến cắt nhau để chứng minh BM = BP, AM = AE, CE = CP.
- Tính chu vi tam giác bằng AB + AC + BC.

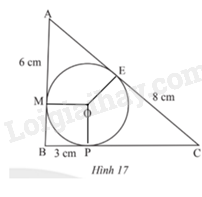
Ta có MB và BP là hai tiếp tuyến tại M và P của đường tròn (O) và cắt nhau tại B.
Advertisements (Quảng cáo)
Do đó: BM = BP = 3cm (Tính chất hai tiếp tuyến cắt nhau).
Ta có AM và AE là hai tiếp tuyến tại M và E của đường tròn (O) và cắt nhau tại A.
Do đó: AM = AE = 6cm (Tính chất hai tiếp tuyến cắt nhau).
Ta có CE và CP là hai tiếp tuyến tại E và P của đường tròn (O) và cắt nhau tại C.
Do đó: CE = CP = 8cm (Tính chất hai tiếp tuyến cắt nhau).
Suy ra chu vi tam giác ABC là:
AB + AC + BC = (AM + MB) + (AE + EC) + (BP + PC)
= (6 + 3) + (6 + 8) + (3 + 8) = 34 cm.
