Bài 5 trang 89 Toán 9 Chân trời sáng tạo tập 1: Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R...

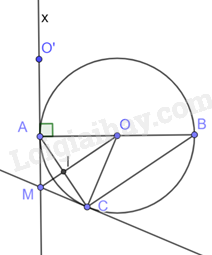
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:

a) \(\widehat {ACB}\) có số đo bằng 90^o, từ đó suy ra độ dài của BC theo R;

b) OM là tia phân giác của \(\widehat {COA}\).

c) MC là tiếp tuyến của đường tròn (O; R).

- Dựa vào dữ kiện đề bài để vẽ hình.

- Tính BC bằng cách áp dụng định lý Pythagore trong tam giác vuông ABC rồi rủ BC theo R.

- Chứng minh OI \( \bot \) AC, tam giác OAC là tam giác cân suy ra OI vừa là trung tuyến và vừa phân giác \(\widehat {COA}\) nên OM là tia phân giác của \(\widehat {COA}\).

- Chứng minh tam giác AOM = tam giác OCM suy ra \(\widehat {OAM} = \widehat {OCM} = {90^o}\). Do đó, MC là tiếp tuyến của đường tròn (O; R).

a) Theo giả thiết ta có \(\widehat {ACB} = {90^o}\)

Áp dụng định lý Pythagore tam giác ABC vuông tại C, ta có:

AB² = AC² + BC² .Do đó BC² = AB² - AC² = (2R)² – R² = 3R²

Mà BC > 0 nên BC = \(R\sqrt 3 \).

b) Ta có IA = IC và AC là dây cung.

Suy ra OI \( \bot \) AC tại I (Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó).

Trong tam giác OAC có OA = OC (= R)

Suy ra tam giác OAC là tam giác cân tại O.

Mà OI là đường trung tuyến của tam giác OAC.

Nên OI cũng là đường phân giác của góc COA

Vậy OM là phân giác \(\widehat {COA}\).

c) Xét \(\Delta \)OAM và \(\Delta \)OCM, ta có:

OA = OC = R

\(\widehat {AOM} = \widehat {COM}\) (Vì OM là phân giác góc AOC)

Cạnh chung OM

Suy ra \(\Delta \)OAM = \(\Delta \)OCM (c.g.c)

Nên \(\widehat {OAM} = \widehat {OCM}\) mà \(\widehat {OAM} = {90^o}\)(AM là tiếp tuyến tại A của (O; R))

Nên \(\widehat {OCM} = {90^o}\).

Do đó: \(MC \bot OM\) tại C.

Vậy MC là tiếp tuyến của đường tròn (O; R).