
Cho đường tròn (O) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) thoả mãn \(\widehat {AMB} = {60^o}\). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.

- Dựa vào dữ kiện đề bài để vẽ hình.
- Chứng minh tam giác AOM = tam giác BMO. Suy ra MA = MB thì tam giác AMB cân tại M
- Chứng minh tam giác AMB đều suy ra độ dài AB từ chu vi tam giác MAB.

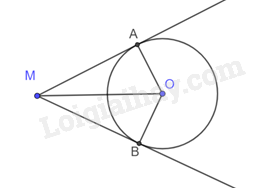
Vì AM, MB là hai tiếp tuyến suy ra \(MA \bot AC;MB \bot BC\).
Advertisements (Quảng cáo)
Xét tam giác vuông AMO và tam giác vuông BMC có:
MO là cạnh chung
OA = OB
Suy ra \(\Delta \)AMO = \(\Delta \)BMC (cạnh huyền – cạnh góc vuông)
Nên MA = MB. Do đó tam giác AMB cân tại M.
Mặt khác, ta có: \(\widehat {AMB} = {60^o}\) nên tam giác AMB đều suy ra AB = MA = MC
Mà AM + AB + MB = \({P_{ABC}}\) = 18
Suy ra 3AB = 18 nên AB = 6 cm.
