
Cho đường tròn (O; 5 cm) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) vuông góc với nhau tại M.
a) Tính độ dài MA và MB.
b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài CD.

- Dựa vào dữ kiện đề bài để vẽ hình.
- Chứng minh tứ giác AOBM là hình vuông suy ra đô dài MA và MB.
- Chứng minh OI \( \bot \) AC, tam giác OAC là tam giác cân suy ra OI vừa là trung tuyến và vừa phân giác \(\widehat {COA}\) nên OM là tia phân giác của \(\widehat {COA}\).
- Chứng minh tam giác OCD cân tại O suy ra OI là đường trung tuyến. Áp dụng tỉ số lượng giác trong tam giác CIO ta tính CI suy ra CD.

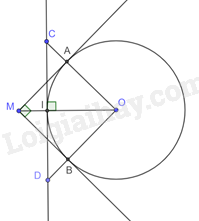
a) Xét tứ giác AOBM có:
\(\widehat {MAO} = {90^o}\) (Vì AM là tiếp tuyến của (O))
\(\widehat {OBM} = {90^o}\)(Vì BM là tiếp tuyến của (O))
Advertisements (Quảng cáo)
\(\widehat {AMB} = {90^o}\) (Vì \(AM \bot MB\) tại M).
Do đó, tứ giác AOBM là hình chữ nhật.
Mà OA = OB (= R của (O))
Nên tứ giác AOBM là hình vuông.
Nên ta có MA = MB = OA = 5 cm.
b) Vì AM và MB là hai tiếp tuyến của (O) cắt nhau tại M nên OM là phân giác của
\(\widehat {AOB}\).
Ta có: \(\widehat {AOM} = \frac{1}{2}.\widehat {AOB} = \frac{1}{2}{.90^o} = {45^o}\)
Xét tam giác OCD có OI là đường cao (vì CI là tiếp tuyến của đường trồn tâm O) và OI là đường phân giác .
Do đó: tam giác OCD cân tại O.
Suy ra OI cũng là đường trung tuyến.
Xét tam giác CIO vuông tại I có CI = OI.tan \(\widehat {COI}\) = 5 .tan 45o = 5 cm.
Mà I là trung điểm của CD (Vì OI là trung tuyến tam giác COD).
Do đó CD = 2CI = 2.5 = 10 cm.
