Bài 6 trang 97 Toán 9 Chân trời sáng tạo tập 1: Xác định số đo các cung \(\overset\frown{AB};\overset\frown{BC};\overset\frown{CA}\) trong mỗi hình vẽ sau...

Xác định số đo các cung \(\overset\frown{AB};\overset\frown{BC};\overset\frown{CA}\) trong mỗi hình vẽ sau:

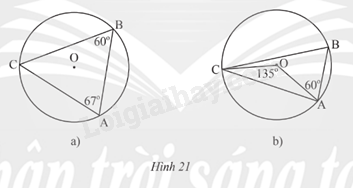
a) Dựa vào định lí: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo cung bị chắn.

b) Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó

Chứng minh tam giác OBA đều suy ra cung AB. Sau đó suy ra cung BC.

a) Xét tam giác ABC, ta có: \(\widehat{ACB}={{180}^{o}}-\widehat{CBA}-\widehat{BAC}={{180}^{o}}-{{60}^{o}}-{{67}^{o}}={{53}^{o}}\)

Ta có sđ\(\overset\frown{AB}\) = 2.\(\widehat{ACB}\) = 2. 53^o = 106^o (Vì \(\overset\frown{AB}\) và \(\widehat{ACB}\) cùng chắn cung AB)

Ta có sđ\(\overset\frown{BC}\) = 2.\(\widehat{BAC}\) = 2. 67^o = 134^o (Vì \(\overset\frown{BC}\) và \(\widehat{BAC}\) cùng chắn cung BC)

Ta có sđ\(\overset\frown{AC}\) = 2.\(\widehat{ABC}\) = 2. 60^o = 120^o (Vì \(\overset\frown{AC}\) và \(\widehat{ABC}\) cùng chắn cung AC).

b) Ta có sđ\(\overset\frown{AC}\) và góc ở tâm \(\widehat{COA}\) cùng chắn cung AC

suy ra sđ\(\overset\frown{AC}\) = \(\widehat{COA}\) = 135^o.

Nối O với B.

Xét tam giác OAB có AO = OB (= R) suy ra tam giác OAB cân tại A.

Mặt khác, \(\widehat {OAB} = {60^o}\) nên tam giác OAB là tam giác đều.

Ta có sđ\(\overset\frown{AB}\) = \(\widehat{AOB}\) = \({{60}^{o}}\) (Vì \(\overset\frown{AB}\) và \(\widehat{AOB}\) cùng chắn cung AB)

Suy ra sđ\(\overset\frown{BC}\) = 360^o - sđ\(\overset\frown{AB}\) - sđ\(\overset\frown{AC}\) = 360^o - \({60^o}\) - 135^o = 165^o.