Câu hỏi/bài tập:

Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Lần lượt vẽ đường tròn (O) đường kính BH và đường tròn (O’) đường kính HC.
a) Xét vị trí tương đối của hai đường tròn (O) và (O’).
b) Đường tròn (O) cắt AB tại E, đường tròn (O’) cắt AC tại F. Chứng minh rằng tứ giác AEHF là hình chữ nhật.
c) Chứng minh rằng EF là tiếp tuyến đường tròn (O) và đồng thời là tiếp tuyến đường tròn (O’).
d) Đường trung tuyến AM của tam giác ABC cắt EF tại N. Cho biết AB = 6 cm, AC = 8 cm. Tính diện tích tam giác ANF.

- Chứng minh OO’ = R + R’ và O; H; H’ thẳng hàng suy ra hai đường tròn tiếp xúc nhau.
- Chứng minh \(\widehat {HEA} = {90^o}\) ; \(\widehat {EAF} = {90^o}\); \(\widehat {AFH} = {90^o}\) suy ra AEHF là hình chữ nhật
- Chứng minh EF \( \bot \) OE suy ra EF là đường trung tuyến đường tròn (O) và EF \( \bot \)O’F suy ra EF là đường trung tuyến đường tròn (O’)
- Cần chứng minh \(\frac{{{S_{\Delta ANF}}}}{{{S_{\Delta EAF}}}} = \frac{{A{F^2}}}{{A{H^2}}}\) suy ra \({S_{\Delta ANF}}\)

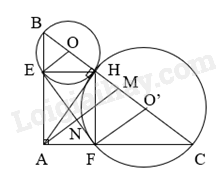
a) Ta có OO’ = OH + O’H = R + R’ và O; H; H’ thẳng hàng.
Suy ra hai đường tròn tiếp xúc nhau.
b) Xét đường tròn (O) có BH là đường kính
là góc nội tiếp chắn cung BH suy ra \(\widehat {BEH}\)= 90o hay AB \( \bot \) EH tại E.
Xét đường tròn (O’) có HC là đường kính
\(\widehat {HFC}\) là góc nội tiếp chắn cung HC suy ra \(\widehat {HFC}\)= 90o hay AC \( \bot \) HF tại F.
Xét tứ giác AEHF có:
\(\widehat {HEA} = {90^o}\) (chứng minh trên);
\(\widehat {EAF} = {90^o}\) (giả thiết);
\(\widehat {AFH} = {90^o}\) (chứng minh trên).
Suy ra tứ giác AEHF là hình chữ nhật.
c) Vì OE = OH = R nên \(\Delta \)OEH cân tại O suy ra \(\widehat {OEH} = \widehat {OHE}\).
Ta có \(\widehat {BHE} = {90^o} - \widehat B\); \(\widehat {BAH} = {90^o} - \widehat B\) suy ra \(\widehat {BHE} = \)\(\widehat {BAH}\).
Mà \(\widehat {OEH} = \widehat {BHE}\) (chứng minh trên); \(\widehat {BHA} = \widehat {AEF}\) (tính chất hình chữ nhật).
Suy ra \(\widehat {OEH} = \widehat {AEF}\) hay \(\widehat {OEH} + \widehat {HEF} = \widehat {AEF} + \widehat {HEF}\) suy ra \(\widehat {OEF} = \widehat {AEH} = {90^o}\).
Nên EF \( \bot \) OE tại E; E \( \in \) (O)
Advertisements (Quảng cáo)
Suy ra EF là đường trung tuyến đường tròn (O) (1).
Vì O’F = O’H = R’ nên tam giác O’HF cân tại O’ suy ra \(\widehat {O’HF} = \widehat {O’FH}\)
Mà \(\widehat {AHF} = \widehat {EFH}\) (tính chất hình chữ nhật)
Nên \(\widehat {O’HF} + \widehat {AFH} = \widehat {O’HF} + \widehat {EFH}\) hay \(\widehat {O’FE} + \widehat {AHC} = {90^o}\).
Nên EF \( \bot \) O’F tại F; F \( \in \) (O’)
Suy ra EF là đường trung tuyến đường tròn (O’) (2).
Từ (1) và (2) ta có điều phải chứng minh.
d) Ta có: \(\widehat {AEF} = \widehat {BAH} = {90^o} - \widehat B\) (tổng ba góc trong của tam giác).
\(\widehat C = {90^o} - \widehat B\) (tổng ba góc trong của tam giác).
Suy ra \(\widehat {AEF} = \widehat {BAH} = \widehat C\) mà \(\widehat C = \widehat {NAF}\) (do AM = MC = BM = \(\frac{1}{2}\) BC nên \(\Delta \) AMC cân tai M).
Suy ra \(\widehat {AEF} = \widehat {NAF}\).
Xét \(\Delta \)ANF và \(\Delta \)EAF có:
\(\widehat {NFA}\) chung
\(\widehat {AEF} = \widehat {NAF}\) (chứng minh trên).
Suy ra \(\Delta \)ANF đồng dạng \(\Delta \)EAF (g – g)
Suy ra \(\frac{{{S_{\Delta ANF}}}}{{{S_{\Delta EAF}}}} = \frac{{A{F^2}}}{{E{F^2}}} = \frac{{A{F^2}}}{{A{H^2}}}\) (EF = AH do AEHF là hình chữ nhật).
Xét \(\Delta \)AEF và \(\Delta \)ABC có:
\(\widehat {EAF}\) chung
\(\widehat {AEF} = \widehat C\) (chứng minh trên).
Suy ra \(\Delta \)AEF đồng dạng \(\Delta \)ABC (g – g)
\(\frac{{{S_{\Delta AEF}}}}{{{S_{\Delta ABC}}}} = \frac{{B{F^2}}}{{B{C^2}}} = \frac{{A{H^2}}}{{B{C^2}}}\) (EF = AH do AEHF là hình chữ nhật).
Ta có \(E{F^2} = A{H^2} = \frac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2}}} = \frac{{{8^2}{{.6}^2}}}{{{8^2} + {6^2}}} = 23,04\) (hệ thức lượng trong tam giác vuông).
Suy ra AH = 4,8 cm.
BC2 = AB2 + AC2 = 62 + 82 =100 (Định lý Pytagore).
Suy ra BC = 10 cm.
AH2 = AF.AC (hệ thức lượng trong tam giác vuông).
Nên \(A{F^2} = \frac{{A{H^2}}}{{AC}} = \frac{{4,{8^2}}}{8}\) = 2,88 cm.
Vậy \(\frac{{{S_{\Delta AEF}}}}{{{S_{\Delta ABC}}}} = \frac{{A{H^2}}}{{B{C^2}}} = \frac{{4,{8^2}}}{{{{10}^2}}} = \frac{{144}}{{625}}\)
suy ra \({S_{\Delta AEF}} = \frac{{144}}{{625}}.{S_{\Delta ABC}} = \frac{{144}}{{625}}.\frac{1}{2}.AB.AC\)= 5,53 cm2.
\(\frac{{{S_{\Delta ANF}}}}{{{S_{\Delta EAF}}}} = \frac{{A{F^2}}}{{A{H^2}}} = \frac{{2,{{88}^2}}}{{4,{8^2}}} = \frac{9}{{25}}\)suy ra \({S_{\Delta ANF}} = \frac{9}{{25}}.{S_{\Delta EAF}}\) = 1,99cm2.
