Câu hỏi/bài tập:

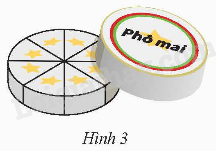
Hộp phô mai hình trụ có đường kính đáy 12,2 cm, chiều cao 2,4 cm.
a) Biết rằng 8 miếng phô mai được xếp nằm sát nhau vừa khít trong hộp (Hình 3). Hỏi thể tích một miếng phô mai là bao nhiêu?
b) Người ta gói từng miếng phô mai bằng một loại giấy đặc biệt. Giả sử phần giấy gói vừa khít miếng phô mai. Hãy tính diện tích phần giấy gói mỗi miếng phô mai.

- Dựa vào công thức thể tích của hình trụ: V = S.h =\(\pi \)r2h
- Dựa vào Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh\)
- Diện tích toàn phần hình trụ \({S_{tp}} = {S_{xq}} + {S_{day}}\) để tính.

a) Bán kính đáy là:
\(R = \frac{d}{2} = \frac{{12,2}}{2} = 6,1\)cm.
Advertisements (Quảng cáo)
Thể tích hộp phô mai là:
V =\(\pi \)R2h = \(\pi .6,{1^2}.2,4 \approx \)281 (cm3).
Thể tích một miếng phô mai là:
281 : 8 = 35 (cm3).
b) Diện tích đáy của cả hộp là:
Sđáy = \(\pi {R^2} = \pi .6,{1^2} \approx \)117 (cm2).
Diện tích xung quanh hình trụ là: :
\({S_{xq}} = 2\pi rh = 2\pi .6,1.2,4 \approx \)92 (cm2).
Diện tích toàn phần của cả hộp là:
\({S_{tp}} = {S_{xq}} + 2{S_{day}} = \)92 + 117.2 \( \approx \) 326 (cm2).
Diện tích toàn phần giấy gói mỗi miếng phô mai là:
S = 326 : 8 = 41 (cm2).
