Bài tập 14 trang 99 Toán 9 tập 2 - Chân trời sáng tạo: Ta coi một ống nghiệm có phần trên là hình trụ và phần dưới là hình cầu (Hình 4)...

Ta coi một ống nghiệm có phần trên là hình trụ và phần dưới là hình cầu (Hình 4). Hãy tính thể tích nước cần để đổ đầy vào ống nghiệm, coi bề dày của ống nghiệm không đáng kể.

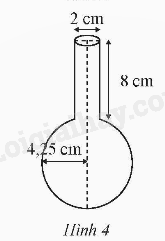
- Dựa vào công thức thể tích của hình trụ: V = S.h =\(\pi \)r²h

- Dựa vào công thức thể tích của hình cầu có bán kính R là: V = \(\frac{4}{3}\pi {R^3}\).

Bán kính phần hình trụ là: \(R = \frac{d}{2} = \frac{2}{2} = 1\) cm

Thể tích phần hình trụ là:

V_trụ =\(\pi \)r²h = \(\pi {.1^2}.8 \approx 25\)(cm³).

Thể tích hình cầu là:

V_cầu = \(\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi .{(4,25)^3} \approx 322\)(cm³).

Thể tích nước cần để đổ đầy bình là:

V = V_trụ + V_cầu \( \approx \) 25 + 322 = 347(cm³).