Câu hỏi Hoạt động 2 trang 67 Toán 9 Chân trời sáng tạo: Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác...

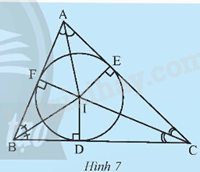
Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7).

a) Chứng minh rằng IE = IF = ID.

b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?

- Xét \(\Delta \) FBI = \(\Delta \) DBI và \(\Delta \) IDC = \(\Delta \) IEC để suy ra IE = IF = ID.

- Nhìn hình và nhận xét.

a) Xét tam giác FBI vuông tại F và tam giác DBI vuông tại D có:

\(\widehat {FBI} = \widehat {IBD}\) (do BI là phân giác góc \(\widehat {FBD}\));

IB chung.

Suy ra \(\Delta \) FBI = \(\Delta \) DBI (cạnh huyền – góc nhọn).

Nên IF = ID (hai cạnh tương ứng) (1).

Xét \(\Delta \) IDC vuông tại D và \(\Delta \) IEC vuông tại E có:

\(\widehat {DCI} = \widehat {IEC}\) (do IC là phân giác góc \(\widehat {DEC}\));

IC chung.

Suy ra \(\Delta \) IDC = \(\Delta \) IEC (cạnh huyền – góc nhọn).

Nên ID = IE (hai cạnh tương ứng) (2).

Từ (1) và (2) suy ra IE = IF = ID.

b) Đường tròn này tiếp xúc với ba cạnh của tam giác tại các điểm F, D, E.