Giải mục 1 trang 10, 11, 12 Toán 9 Chân trời sáng tạo tập 1: Hỏi 20oC tương ứng bao nhiêu độ F?...

Hoạt động1

Trả lời câu hỏi Hoạt động 1 trang 10

Để chuyển đổi từ độ F ( kí hiệu x) sang độ C (ký hiệu y), ta dùng công thức:

$y = \frac{5}{9}(x - 32)$

a) Biến đổi công thức trên về dạng x – 1,8y = 32.(1)

b) Hỏi 20^oC tương ứng bao nhiêu độ F?

c) Hỏi 98,6^oF tương ứng bao nhiêu độ C?

- Biến đổi cho x,y về cùng 1 vế, hằng số 1 vế

- Rút x theo y thay vào tính ra kết quả rồi kết luận

- Rút y theo x thay vào tính ra kết quả rồi kết luận

a) Ta có $y = \frac{5}{9}(x - 32)$

$9y = 5(x - 32)$

$\begin{array}{l}5x - 9y = 160\\x - 1,8y = 32\end{array}$

b) x – 1,8y = 32

$\begin{array}{l}x = 32 + 1,8y\\x = 32 + 1,8.20\\x = 68\end{array}$

Vậy 20^oC tương ứng 68^oF.

c) Ta có $y = \frac{5}{9}(x - 32)$

$y = \frac{5}{9}(98,6 - 32) = 37$

Vậy 98,6^oF tương ứng 37^oC.

Thực hành1

Trả lời câu hỏi Thực hành 1 trang 12

Xác định các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau:

a) x + 5y = -4

b) $\sqrt 3 x + y = 0$

c) $0x - \frac{3}{2}y = 6$

d) 2x + 0y = - 1,5.

Dựa vào khái niệm phương trình bậc nhất hai ẩn x và y là hệ thức có dạng

$ax + by = c$

Trong đó, a và b không đồng thời bằng 0.

a) a = 1; b = 5; c = -4

b) a = $\sqrt 3$; b = 1; c = 0

c) a = 0; b = $- \frac{3}{2}$; c = 6

d) a = 2; b = 0; c = - 1,5.

Thực hành2

Trả lời câu hỏi Thực hành 2 trang 12

Cho phương trình 3x + 2y = 4. (1)

a) Trong 2 cặp số (1;2) và (2;-1), cặp số nào là nghiệm của phương trình(1)?

b) Tìm y_o để cặp số (4;y_o) là nghiệm của phương trình (1).

c) Tìm thêm 2 nghiệm của phương trình (1).

d) Hãy biểu diễn tất cả các nghiệm của phương trình (1) trên mặt phẳng toạ độ Oxy.

- Thay lần lượt 2 cặp số vào phương trình (1) cái nào thoả mãn thì chính là nghiệm.

- Thay x = 4 và phương trình để tìm ra y_o.

- Cho x bất kì rồi tìm ra y

- Dựa vào VD3 trang 11 để vẽ các nghiệm trên mặt phẳng toạ độ Oxy.

a) Thay cặp số (1;2) vào (1) ta có:

3.1 + 2.2 = 7 $\ne$ VP. Vậy (1;2) không phải nghiệm của (1)

Thay cặp số (2;-1) vào (1) ta có: 3.2 + 2.(-1) = 4 = VP. Vậy (2;-1) là nghiệm của (1).

b) Thay x = 4 vào (1) ta có:

3.4 + 2y = 4

Suy ra ${y_o} = \frac{{4 - 12}}{2} = - 4$.

c) Ta có

$\begin{array}{l}3x + 2y = 4\\y = \frac{{4 - 3x}}{2}\end{array}$

Cho x = 0 suy ra $y = 2$. Vậy (0;2) là nghiệm của phương trình (1).

Cho x = 1 suy ra $y = \frac{1}{2}$. Vậy (1; $\frac{1}{2}$) là nghiệm của phương trình (1).

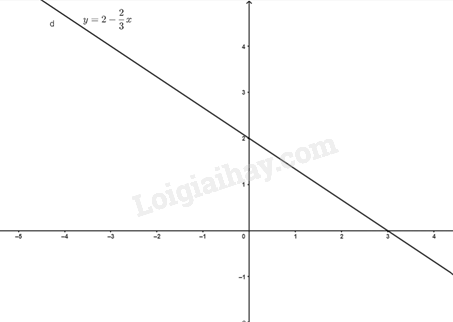
d) Viết lại phương trình thành $y = \frac{{4 - 3x}}{2} = 2 - \frac{3}{2}x$. Từ đó, tất cả các nghiệm đã cho được biểu diễn bởi đường thẳng d: $y = 2 - \frac{3}{2}x$.