Giải mục 1 trang 37, 38, 39 Toán 9 Chân trời sáng tạo tập 1: Thay mỗi ? bằng số thích hợp để có các đẳng thức...

Hoạt động1

Trả lời câu hỏi Hoạt động 1 trang 37

Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.

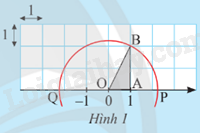
a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.

b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.

Gọi x là số thực được biểu diễn bởi điểm P, y là số thực được biểu diễn bởi điểm Q.

Thay mỗi ? bằng số thích hợp để có các đẳng thức:

x² = ?, y² = ?.

Dựa vào định lý Pythagore trong tam giác OAB là OB² = OA² + AB² để tìm OB.

a) Áp dụng định lí Pythagore vào tam giác vuông OAB ta có:

OB = $\sqrt {1 + {2^2}} = \sqrt 5$

b) Vì P, Q là hai điểm thuộc đường tròn tâm O bán kính OB nên $OP = OQ = OB = \sqrt 5$

Vì x là số thực được biểu diễn bởi điểm P nên $x = \sqrt 5$,

y là số thực được biểu diễn bởi điểm Q nên $y = -\sqrt 5$.

Khi đó ta có các đẳng thức:

${x^2} = {\left( {\sqrt 5 } \right)^2} = 5$

${y^2} = {\left( {-\sqrt 5 } \right)^2} = 5$

Thực hành1

Trả lời câu hỏi Thực hành 1 trang 38

Tính các căn bậc hai của mỗi số sau:

a) 36

b) $\frac{4}{{49}}$

c) 1,44

d) 0

Dựa vào VD1 trang 38 và làm tương tự.

a) Ta có 6² = 36, nên 36 có hai căn bậc hai là 6 và – 6

b) Ta có ${\left( {\frac{2}{7}} \right)^2}$= $\frac{4}{{49}}$, nên $\frac{4}{{49}}$ có hai căn bậc hai là $\frac{2}{7}$ và - $\frac{2}{7}$

c) Ta có (1,2)² = 1,44 nên 1,44 có hai căn bậc hai là 1,2 và – 1,2

d) Số 0 chỉ có một căn bậc hai là chính nó $\sqrt 0 = 0$

Thực hành2

Trả lời câu hỏi Thực hành 2 trang 38

Sử dụng dấu căn bậc hai để viết các căn bậc hai của mỗi số:

a) 11

b) 2,5

c) – 0,09

Dựa vào VD2 trang 38 làm tương tự.

a) Các căn bậc hai của 11 là $\sqrt {11}$ và - $\sqrt {11}$

b) Các căn bậc hai của 2,5 là $\sqrt {2,5}$ và - $\sqrt {2,5}$

c) Do – 0,09 là số âm nên nó không có căn bậc hai.

Thực hành3

Trả lời câu hỏi Thực hành 3 trang 38

Tính

a) $\sqrt {1600}$

b) $\sqrt {0,81}$

c) $\sqrt {\frac{9}{{25}}}$

Dựa vào VD3 trang 38 và làm tương tự.

a) $\sqrt {1600} = \sqrt {{{40}^2}} = 40$

b) $\sqrt {0,81} = \sqrt {{{(0,9)}^2}} = 0,9$

c) $\sqrt {\frac{9}{{25}}} = \sqrt {{{\left( {\frac{3}{5}} \right)}^2}} = \frac{3}{5}$

Thực hành4

Trả lời câu hỏi Thực hành 4 trang 39

Tính giá trị của các biểu thức:

a) ${\left( {\sqrt {12} } \right)^2}$

b) ${\left( { - \sqrt {0,36} } \right)^2}$

c) ${\left( {\sqrt 5 } \right)^2} + {\left( { - \sqrt {1,21} } \right)^2}$

Dựa vào VD4 trang 38 và làm tương tự.

a) ${\left( {\sqrt {12} } \right)^2} = 12$

b) ${\left( { - \sqrt {0,36} } \right)^2} = 0,36$

c) ${\left( {\sqrt 5 } \right)^2} + {\left( { - \sqrt {1,21} } \right)^2} = 5 + 1,21 = 6,21$

Vận dụng1

Trả lời câu hỏi Vận dụng 1 trang 39

Biết rằng hình A và hình vuông B trong Hình 2 có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B.

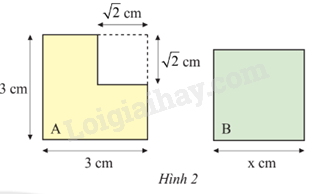
Tính diện tích hình vuông to trừ đi diện tích hình vuông nhỏ tìm được diện tích hình A.

Từ diện tích hình A suy ra diện tích hình B rồi ta tìm x.

Xét hình A:

Ta có diện tích cả hình vuông cạnh 3cm là : 3.3 = 9 cm²

Ta có diện tích cả hình vuông cạnh $\sqrt 2$ cm là : $\sqrt 2$. $\sqrt 2$ = 2 cm²

Suy ra diện tích hình A là: 9 – 2 = 7 cm²

Mà hình vuông B bằng diện tích hình A là 7 cm²

Nên x.x = x² = 7 suy ra x = $\sqrt 7$ cm.