Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 76
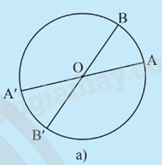
a) Cho đường tròn (O;R).
i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA’.
ii) Lấy điểm B khác A thuộc đường tròn (O;R). Tìm điểm B’ sao cho O trung điểm của đoạn thẳng BB’. Điểm B’ có thuộc đường tròn (O;R) không? Giải thích.
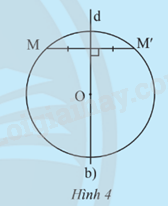
b) Cho đường tròn (O;R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (khi M thuộc d thì lấy M’ trùng với M). Điểm M’ có thuộc đường tròn (O;R) không? Giải thích.

Dựa vào khái niệm đường tròn để giải thích: Đường tròn tâm O bán kính R (R > 0) là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.

a)
i) O là trung điểm của đoạn thẳng AA’ vì trong đường tròn (O;R): Hai điểm A và A’ đều cách điểm O một khoảng bằng R.
ii) Điểm B’ nằm đối xứng với B qua điểm O.
Điểm B’ cũng thuộc đường tròn (O;R) vì B nằm cách O một khoảng R nên B’ nằm cách O một khoảng R suy ra OB = OB’.
b) Điểm M’ cũng thuộc đường tròn (O;R) vì M’ là điểm đối xứng với M qua trung trực d.
Thực hành1
Trả lời câu hỏi Thực hành 1 trang 77
Advertisements (Quảng cáo)
Xác định tâm đối xứng và trục đối xứng của bánh xe trong Hình 7. Giải thích cách làm.


Dựa vào tính đối xứng của đường tròn:
+ Tâm đối xứng là tâm của đường tròn
+ Mọi đường thẳng đi qua tâm của đường tròn đều là trục đối xứng của nó.

Tâm đối xứng của bánh xe là trục ở giữa. (Đường tròn có 1 tâm đối xứng)
Trục đối xứng của bánh xe là đường thẳng đi qua trục ở giữa (Đường tròn có vô số tâm đối xứng).
Vận dụng1
Trả lời câu hỏi Vận dụng 1 trang 77
Nêu cách chia một cái bánh có dạng hình tròn tâm O (Hình 8) thành hai phần bằng nhau.


Xác định một trục đối xứng của bánh.

Vẽ một trục đối xứng đi qua tâm O để chia bánh thành 2 phần bằng nhau.
